主題:幾何學
外觀
幾何學

幾何學出現於處理空間關係的知識領域。幾何學是前現代數學的兩個領域之一,另一個是數字的研究。
在近代,幾何學概念已經被擴展。它們有時顯示高水平的抽象和複雜性。幾何學現在使用微積分學和抽象代數的方法,從而使該領域的許多現代分支不容易被辨認出是早期幾何學的後代(見數學領域)。工作於或者是專業從事於幾何學的人是幾何學家。
特色條目
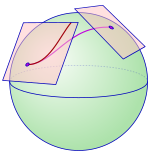
仿射聯絡是微分幾何中定義在流形上的幾何概念,連接了鄰近幾點上的切空間,使得在流形上的切向量場可以求導。仿射聯絡的概念起源於19世紀的幾何學和張量微積分,但那時並沒有被完備的定義出來。直到1920年,(用於嘉當聯絡(Cartan connection)理論)及Hermann Weyl(做為廣義相對論的基礎理論)。這專門術語是沿用嘉當(Cartan)所使用的術語及根據從歐幾里德空間Rn中切空間的推廣。換句話說,仿射聯絡的概念是為了推廣歐幾里德空間,使得流形上每點都有一個光滑的(可無限求導)仿射空間。
任何維數為正數的流形都會有無窮個仿射聯絡。仿射聯絡能用來決定在向量場上求導,並滿足線性及萊布尼茲法則的方法,這表明了仿射聯絡有幾個可行的方法,像是協變導數或在向量叢上的聯絡。仿射聯絡也能用來決定在切向量沿著一條曲線平行移動的方式,或者用來決定標架叢的平行移動。仿射聯絡也可以用來決定流形上的測地線,推廣了歐幾里德空間中直線的概念。
相關專題
歡迎參與

- 歡迎改進或擴充的條目 :
- 請求條目:
- 欄目特色圖片, 和精選傳記
- 幾何學綱要、幾何學歷史、合成幾何學、幾何學議題列表、廣義三角函數
- 超矩形、手性 (數學)、偽三角形、抽象多胞形,考克斯特符號、考克斯特元素、421多胞形、E8、錐面、一萬邊形
- 凸幾何、轉換幾何、代數曲面、Gröbner基、實代數幾何、複幾何
- 模板: Template:Honeycombs、Template:Tessellation、Template:Mathematics and art(數學和藝術)
- 需要繼續擴充或翻譯的條目:
- 需要專家關注
- 張量(tensor)
你知道嗎?
分類
以下的分類樹顯示Category:幾何學下的分類。