主题:几何学
外观
几何学

几何学出现于处理空间关系的知识领域。几何学是前现代数学的两个领域之一,另一个是数字的研究。
在近代,几何学概念已经被扩展。它们有时显示高水平的抽象和复杂性。几何学现在使用微积分学和抽象代数的方法,从而使该领域的许多现代分支不容易被辨认出是早期几何学的后代(见数学领域)。工作于或者是专业从事于几何学的人是几何学家。
特色条目
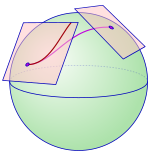
仿射联络是微分几何中定义在流形上的几何概念,连接了邻近几点上的切空间,使得在流形上的切向量场可以求导。仿射联络的概念起源于19世纪的几何学和张量微积分,但那时并没有被完备的定义出来。直到1920年,(用于嘉当联络(Cartan connection)理论)及Hermann Weyl(做为广义相对论的基础理论)。这专门术语是沿用嘉当(Cartan)所使用的术语及根据从欧几里德空间Rn中切空间的推广。换句话说,仿射联络的概念是为了推广欧几里德空间,使得流形上每点都有一个光滑的(可无限求导)仿射空间。
任何维数为正数的流形都会有无穷个仿射联络。仿射联络能用来决定在向量场上求导,并满足线性及莱布尼兹法则的方法,这表明了仿射联络有几个可行的方法,像是协变导数或在向量丛上的联络。仿射联络也能用来决定在切向量沿着一条曲线平行移动的方式,或者用来决定标架丛的平行移动。仿射联络也可以用来决定流形上的测地线,推广了欧几里德空间中直线的概念。
相关专题
欢迎参与

- 欢迎改进或扩充的条目 :
- 请求条目:
- 栏目特色图片, 和精选传记
- 几何学纲要、几何学历史、合成几何学、几何学议题列表、广义三角函数
- 超矩形、手性 (数学)、伪三角形、抽象多胞形,考克斯特符号、考克斯特元素、421多胞形、E8、锥面、一万边形
- 凸几何、转换几何、代数曲面、Gröbner基、实代数几何、复几何
- 模板: Template:Honeycombs、Template:Tessellation、Template:Mathematics and art(数学和艺术)
- 需要继续扩充或翻译的条目:
- 需要专家关注
- 张量(tensor)
你知道吗?
分类
以下的分类树显示Category:几何学下的分类。