Talbot曲线
外观
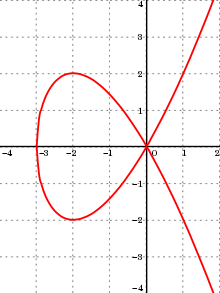

Talbot曲线也称为切恩豪斯立方曲线,为一平面曲线,极坐标方程式如下
Talbot曲线是 n = −1/3的正弦螺线。
历史
[编辑]埃伦弗里德·瓦尔特·冯·切恩豪斯、纪尧姆·德·洛必达及欧仁·查尔斯·加泰罗尼亚都曾研究此曲线。在R C Archibald于1900年发表的论文中将此称为切恩豪斯立方曲线,不过也称为洛必达立方曲线(de L'Hôpital's cubic)或加泰罗尼亚三等分角线(trisectrix of Catalan)。
其他方程式
[编辑]令,再应用棣莫弗公式可得
可以得到此曲线的参数式。参数t可以消去,得到以下方程式
- .
若此参数式水平平移8a,方程式会变成
或
- .
因此可以得到另一个极坐标方程式
- .
参考资料
[编辑]- J. D. Lawrence, A Catalog of Special Plane Curves. New York: Dover, 1972, pp. 87-90.












