勒萨吉重力理论
勒萨吉重力理论(英语:Le Sage's Theory of Gravitation)是一种关于重力的动力学理论,最早由尼古拉·法蒂奥·丢勒在1690年提出,随后又由乔治-路易斯·勒萨吉在1748年重新提出。该理论借助微小不可见的粒子的流动,对牛顿的万有引力提出了一种机械解释[1]。这种微粒勒萨吉称之为“超凡小体”(ultra-mundane corpuscles),它们会从各个方向撞击一切物体。根据这种模型,任两个物体都相互遮蔽了一些撞向它们的小体,因此小体撞击物体的静压力会不平衡,导致两个物体相互靠近。这种对重力的机械解释从未得到广泛认可。
基本理论
[编辑]
该理论认为,重力是宇宙中的一种微粒(小体)朝各个方向高速运动的结果。理论假定微粒朝各个方向流动的强度完全相同,因此一个孤立物体 A 会被从各个方向以相同的力撞击,只会有向内的压力而不会有净推力(见图 1)。
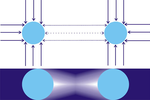
但是,如果有第二个物体 B 在场,本来会从 B 的方向撞击 A 的一小部分粒子就会被拦截,因此 B 就起到了屏蔽的作用,在 B 所在的方向上,A 受到的粒子撞击会比反方向少一些。类似地,在 A 所在的方向上,B 受到的粒子撞击也会比反方向少一些。我们可以说 A 和 B 相互“遮蔽”,而这两个物体会因为撞击力的不平衡而被推向彼此(见图 2)。因此,根据勒萨吉的理论,这种物体之间的表象上的吸引力,实际上是因为从另一物体的方向而来的推力减小。故而这种理论有时被称为“推力重力”(push gravity)或者“遮蔽重力”(shadow gravity),虽然它更常被叫做“勒萨吉重力”(Le Sage Gravity)。
碰撞的本性
[编辑]
如果物体 A 和重力微粒的撞击是完全弹性碰撞,则从物体反射的微粒强度将会和入射微粒相同,因此不可能会有净推力。但是,这件事即使在引入第二个物体 B 时也会是对的。虽然 B 起到了屏蔽的作用,使本来会撞向 A 的重力微粒被 B 挡住,但是会有别的本来不会撞上 A 的粒子,在经过撞击 B 改变方向后,替代那些本来应该撞向 A 的粒子。因此如果这种碰撞是完全弹性的,那么在 A 和 B 之间反射的粒子就会完全补偿遮蔽作用。所以,如果要产生净重力,就必须要假设这种碰撞不是完全弹性的,或至少有一部分反射回来的粒子变慢了,它们的动量将比撞击前少。如此一来,对单个物体 A,会有一些粒子以减弱的动量离开 A,另一些粒子以未减弱的动量抵达 A,最终会产生一个指向 A 物体中心的净动量(见图 3)。在这种假设中,两个物体间反射的粒子就不会完全补偿遮蔽作用,因为反射流比入射流会弱一些。
平方反比定律
[编辑]
由于我们假设撞击在物体上的一些(或全部)重力微粒被该物体吸收(或减慢),因此从物体处散发出去的重力微粒的通量强度,将小于指向该物体的重力微粒。我们可以想像这种动量流的不平衡,及由此产生的施加在附近其他物体上的力的不平衡,会均匀分布在以物体为中心的球形表面上(见图 4)。在包围物体的球形表面上,动量流不平衡的程度与包围球的大小无关,而球形的表面积则按半径的平方成比例增加。因此,每单位面积上的动量不平衡,会与距离的平方成反比。
与质量成正比
[编辑]从目前概述了的几个前提来看,重力微粒只能产生与物体表面积成比例的力。但是引力却应该与质量成正比。为了满足与质量成正比的需求,勒萨吉理论认为:一)物质的基本元素很小,因此整个物体主要由空白空间组成; 二)重力微粒非常微小,因此只有很小一部分会被物质拦截。因此,每个物体内部的“遮蔽部分”与物质的每个基本元素的表面积成正比。如果接着假设物质不可穿透的基本元素都是相同的(即密度与表面积的比率相同),那么遮蔽效果就会(至少是近似)与质量成正比(图 5)。

法蒂奥
[编辑]
尼古拉·法蒂奥在其 1690 年春天写给克里斯蒂安·惠更斯的信中,第一次对他的重力理论做出表述。[2]两天后,法蒂奥在伦敦皇家学会宣读了这封信的内容。在接下来的几年中,法蒂奥撰写了他的主要著作《论重力的成因》(De la Cause de la Pesanteur)的几段手稿,但这些材料在他生前没有出版过。1731 年,法蒂奥还以卢克莱修的风格把他的理论谱写成拉丁语诗作寄给了巴黎科学院,但被退稿了。前述手稿的一些片段,以及这首诗的副本,后来被勒萨吉得到,但他未能找到愿意出版法蒂奥论文的出版商。[3]直到 1929 年,卡尔·博普(Karl Bopp)才出版了法蒂奥手稿的唯一完整复本[4],而到了 1949 年,加涅宾(Gagnebin)才使用勒萨吉收集的片段来重建论文[5]。加涅宾版包含了法蒂奥在 1743 年以前做的全部修订,这距他撰写博普那份复本所依据的草稿已有 40 年了。但是,博普版的后半部分包含法蒂奥理论中数学上最先进的部分,但加涅宾并未将其包括在内。有关法蒂奥作品的详细分析,以及博普版和加涅宾版副本之间的比较,请参见 Zehe 的著作[6]。以下描述主要基于博普版。
法蒂奥理论的特点
[编辑]法蒂奥的金字塔(问题 I)
[编辑]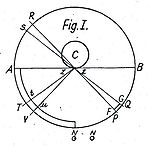
法蒂奥假设宇宙中充满了微小的粒子,这些粒子以极高的速度在各个方向上直线移动。为了描述他的想法,他使用了下面一个例子:假设有个物体 C,在其上画出无限小的平面 zz,和以 zz 为中心的球体。 法蒂奥在此球体中放置了金字塔 PzzQ,其中一些粒子沿 zz 方向流过,还有一些粒子已经被 C 反射,并因此离开 zz。 法蒂奥认为反射粒子的平均速度比入射粒子低,因此其动量也较弱,故会产生某种流,将所有物体推向 zz 方向。一方面,流的速度保持恒定,但另一方面,与 zz 的距离越近,流的密度就越高,因此其强度与 1/r2 成正比。由于可以在 C 周围绘制无限数量的这种金字塔,因此这一比例适用于 C 附近的整个范围。
微粒速度的减少
[编辑]为表明粒子在反射后行进速度会减小的假设合理,法蒂奥进一步陈述了以下假设:
陈述这些假设的段落是法蒂奥理论中最费解的部分,因为他没有清晰表明他觉得哪一种碰撞方式更合理。但是,在他理论 1742 年的新版中,他缩短了相关的段落,将“完全弹性或弹力”归给颗粒,另一方面将“不完全弹性”归给物体。依此,微粒会以减弱的速度反射。法蒂奥还面临另一个问题:如果这些微粒互相碰撞会发生什么事?非弹性碰撞将导致粒子速度稳定下降,从而导致重力降低。为了避免该问题,法蒂奥假定粒子的直径与其相互间的距离相比非常的小。
微粒的凝聚
[编辑]法蒂奥长期以来一直认为,由于这些微粒接近物体的速度高于(反射之后)远离物体的速度,微粒会在物体附近不断积累(他称这种现象为“凝聚”)。但是,他后来意识到,尽管进入的微粒更快,但它们之间的间隔也会比反射的微粒更远,因此向内和向外的总粒子流相等。因此,微粒的长期积累不存在,反射微粒的密度保持恒定(假设这些微粒足够小,在物体附近不会发生明显的相互碰撞)。更重要的推论是,法蒂奥指出,通过同时增加微粒的速度和弹性,可以任意减小入射和反射微粒的速度(以及密度)之间的差异,同时仍保持相同的等效重力。
物体的空隙
[编辑]
为确保这种重力会和质量成正比,法蒂奥假设微粒流动对物体的穿透性非常高。他简述了三种模型来表达该假设是对的:
- 他认为一切物体都是某种“小球”的积聚物,这些“球”的直径与它们彼此之间的距离相比“无限”小。但是他拒绝了这一提议,因为在这种情况下,物体之间会互相接近,不会保持稳定。
- 他又假设这些球可以通过杆或线连接起来,并会形成某种晶体结构。但是,他也拒绝了该模型——如果多个小球在一起,那么重力微粒的流体将无法在所有方向上均等地穿透该结构,因此重力不可能与质量成正比。
- 最后,法蒂奥把这些球去掉,只留下了杆或者说它们组成的网格。通过使它们“无限地”小于它们彼此之间的距离,就能实现最大的可穿透性。
微粒的压力(问题 II)
[编辑]在 1690 年法蒂奥就假定,微粒在平面上施加的“推力”是这种重力理论的第六部分,如果所有粒子都垂直于平面就会产生这种推力。法蒂奥通过计算该力的大小来证明自己的推测。该力被施加在某个点 zz 上。他推导出如下公式:p = ρv2zz/6。这个解和气体动力论中为人熟知的公式 p = ρv2/3 非常像,而后者是由丹尼尔·伯努利在 1738 年提出的。这是第一次有人指出一种和气体动力论可相类比的解——远在后者理论中的基本概念发展之前。 但是,伯努利的压力值比法蒂奥大两倍。根据 Zehe 的研究,这是因为法蒂奥将碰撞后的动量变化计算成 mv 而非 2mv,因此得到了错误结论,他的结果只对完全非弹性碰撞正确。 法蒂奥不只试图将这种解用来解释重力,还想用于解释气体的行为。他试图构造一个温度计,能指出空气分子的“运动状态”,从而可以估算温度。但是法蒂奥(与伯努利不同)没有发现热和空气的运动是“相同”的——他用另一种流体来解释空气分子的运动。伯努利是否受到法蒂奥的影响是未知的。
无限(问题 III)
[编辑]在这一章中,法蒂奥研究了“无限”这一术语与其理论之间的关系。 法蒂奥经常以某些现象比其他现象“无限小或无限大”的事实来证明他的想法是正确的,在这种情况下,很多问题就可以减小到无法探测可以忽略的值。例如,晶体结构中杆的直径无限小于彼此之间的距离,或粒子的速度比物体的速度无限大,或反射和非反射粒子之间的速度差无限小。
介质的阻力(问题 IV)
[编辑]这是法蒂奥的理论中,在数学上最复杂的部分。在这一章他试图估计微粒流对移动中的物体产生的阻力。假定 u 是物体的速度,而 v 是重力微粒的速度,ρ 是微粒介质的浓度。在 v ≪ u 并且 ρ 是一个常数的情况下,法蒂奥计算出阻力为 ρu2。在 v ≫ u 且 ρ 是一个常数的情况下,阻力则是 4/3ρuv。牛顿指出天体的轨道运动不应受到这种阻力影响,这要求空间中的任何介质都必须非常稀疏。因此法蒂奥减小了微粒的密度,并指出为了维持足够的重力,粒子密度的减小应该要由“依密度的平方反比”增加 v 来补偿。这是从法蒂奥的粒子压力理论得到的,这一压力正比于 ρv2。根据 Zehe 的研究,法蒂奥只要试图把 v 增大到非常高的值,实际上就能够使这种阻力(相对于重力而言)非常小,因为在法蒂奥的模型里,阻力在此时正比于 ρuv 但是重力(即微粒带来的压力)正比于 ρv2。
法蒂奥理论的反响
[编辑]法蒂奥曾和与他同一时代的最著名的科学家之间进行过交流。

在1690年至1693年之间,艾萨克·牛顿与法蒂奥之间有牢固的个人关系。牛顿对法蒂奥理论的陈述差异很大。例如,1962 年,在牛顿自己持有的《原理》(Principia)印刷复本中,他在描述了对重力的机械解释的必要条件以后,写下了一段(未出版的)注解:“然而唯一可以解释重力的[机械]假设就是这种假设,而这种解释则由最灵巧的几何学家 N. Fatio 先生首次设计出来”[6]。另一方面,法蒂奥本人则表示,尽管牛顿私下评论说法蒂奥的理论是对其引力最好的机械解释,他自己清楚牛顿倾向于相信引力的真正解释不是机械的。另外,数学家格里高利在他的《备忘录》(Memoranda)中指出:“牛顿先生和哈雷先生嘲笑法蒂奥先生解释重力的方式。” [6]据称,这是他在 1691 年 12 月 28 日注意到的。但是,他实际写下这段话的日期却是未知的,因为使用的墨水和羽毛都与页面的其余部分不同。1694 年后,牛顿与法蒂奥两人的关系逐渐淡化。
克里斯蒂安·惠更斯是最早获知法蒂奥理论的人,但他从未接受。法蒂奥相信他已经说服了惠更斯其理论是一致的,但是惠更斯在给哥特佛莱德·莱布尼兹的信中否认了这一点。法蒂奥和莱布尼兹之间在理论上也有短暂的往来。莱布尼兹出於哲学理由拒绝在微粒间留出空隙,因此批评了法蒂奥的理论。 雅各布·伯努利对法蒂奥的理论表示有兴趣,并敦促法蒂奥用完整的手稿来写他的引力思想,而法蒂奥实际写了一份。伯努利克隆了该手稿,现在存于巴塞尔大学图书馆中,并且是前述的博普版复本的基础。
虽然法蒂奥和这些科学家都有交流,除了克拉默和勒萨吉等,其理论仍然不为人知。这是因为法蒂奥从未能够正式出版自己的作品,而且他受到了一群宗教狂热分子的影响,他们被人称作“法国先知”(属于卡米撒派),这使得他的公众声誉遭受破坏。
克拉默与雷德克
[编辑]1731 年,瑞士数学家加布里尔·克拉默(Gabriel Cramer)发表了一篇论文,[7] 末尾出现了与法蒂奥理论非常相似的理论纲要——包括物质的网状结构,重力和光的类比,以及遮蔽作用——但没有提及法蒂奥的名字。 法蒂奥知道克拉默能够得到他主要论文的副本,因此指责克拉默只是重复他的理论且没能够读懂。不过,勒萨吉同样是经克拉默告知,才在 1749 年知道法蒂奥的理论。1736 年,德国医生弗朗兹·阿尔伯特·雷德克(Franz Albert Redeker)也发表了类似的理论。[8]尚未知晓雷德克和法蒂奥之间存在的任何关系。
勒萨吉
[编辑]
勒萨吉第一次阐述自己的理论,是在 1748 年,他将自己的论文《论死力的起源》(Essai sur l'origine des forces mortes)[9]提交予位于巴黎的法国科学院,但该论文从未被出版。[3]根据勒萨吉自己的说法,是在他写出并发表这份论文之后,他才知道法蒂奥、克拉默和雷德克的理论。勒萨吉的理论阐述第一次出版,则是在 1756 年,[10]。1758 年,在他参与位于卢昂(Rouen)的法国科学院举办的竞赛时,提交了一篇更细致的论文,《论化学力学》(Essai de Chymie Méchanique)[11] 。在这篇文章中他试图同时解释重力和化学亲和力的本性。公众获知该理论,则要到 1784 年,他出版《牛顿式的卢克莱修》(Lucrèce Newtonien),在该文中他将他理论和卢克莱修观念的对应关系发展成熟。[12] 另一篇关于其理论的阐述,则是在他死后,由皮耶尔·普瑞弗斯特在 1818 年出版。[13]
勒萨吉的基本概念
[编辑]
勒萨吉非常详细地讨论了自己的理论,并且提供了对理论部分参数所做的定量估计。
- 他把重力微粒叫做超凡小体,因为他假定这些小体来自我们已知的宇宙之外。超凡小体的流动分布是各向同性的,而其传播的规律则和光非常相似。
- 勒萨吉认为如果一般物体和微粒的碰撞是完全弹性的,就不会有任何重力。因此他假定这些微粒和物体的基本组成成分是“绝对坚硬”的,并断言由此可以得出相当复杂的相互作用形式——如果微粒从垂直于一般物体表面的方向碰撞,那就是完全非弹性的,如果从其表面的切线方向碰撞,就是完全弹性的。他随后评注这蕴含了散射微粒的平均速度会是入射微粒的 2/3。为了避免微粒之间的非弹性碰撞,他假定微粒的直径相对于它们之间的距离非常小。
- 微粒流带来的阻力正比于 uv(v是微粒的速度而u是物体的速度),而引力则正比于v2,因此只要提高v的值,阻力和重力之比就可以任意地小。因此,他认为“超凡小体”可能以光速运动。但在进一步考量后,他又把这个数值调整为光速的 105 倍。
- 为保证重力和质量成正比,推断一般物体由笼状结构组成,其节点直径只有它们相互距离的 107 分之一,而组成笼状结构的“杆”相对于笼状结构本身也非常小(其长度是厚度的 1020 倍),因此微粒可以在几乎没有被阻拦的情况下穿过物体。
- 勒萨吉也试图用遮蔽机制来解释凝聚力的存在,以及不同强度的其他力,他假定超凡小体有多种类型,彼此尺寸不同,如图 9 所示。
勒萨吉宣称他是第一个得出这种理论所有结论的人,普瑞弗斯特也认为勒萨吉的理论比法蒂奥的理论更成熟。[3] 但是,在对法蒂奥的论文(勒萨吉也拥有这些论文)进行细致分析之后,Zehe 比较了两人的理论,判断勒萨吉没有做出实质上的新贡献,而且他常常没有达到法蒂奥的推论深度。[6]
勒萨吉理论的反响
[编辑]勒萨吉的观念在他的时代并没有获得正面评价,除了他的少数朋友和同僚,例如皮耶尔·普瑞弗斯特,夏勒·博内(Charles Bonnet),尚-安德烈·德吕克(Jean-André Deluc),查尔斯·斯坦厄普(Charles Mahon, 3rd Earl Stanhope),以及赛门·留利尔(Simon Lhuilier)。他们在他们的著作和论文中提及并描述了勒萨吉的理论,曾为他们的同代人用作理解勒萨吉理论的二手信源(因为勒萨吉本人出版的论文甚少)。
欧拉、伯努利与博什科维奇
[编辑]李昂哈德·欧拉在 1761 年曾经评论勒萨吉的理论比其他作者的理论都来得“无限地好”,而所有反驳都被这一模型抵消,但接下来就说该理论和光的类比对他而言毫无重量,因为他相信光的本性是波动。在进一步考量下,欧拉基本拒绝了该理论,并在 1765 年写信给勒萨吉说:[14]
| “ | 先生,请原谅我,如果我对您超凡小体的理论感到非常不耐,因为我总是更偏好坦承我对重力成因的无知,而不是诉诸这些奇怪的假设。 | ” |
丹尼尔·伯努利乐于见到勒萨吉理论与其对气体本性的想法间的相似性。但是,伯努利认为自己的气体动力论只不过是一种推测,因此类似地也认为勒萨吉的理论是高度推测性的。[15]
罗杰·约瑟夫·博什科维奇(Roger Joseph Boscovich)指出,勒萨吉理论是第一个能实际用机械过程解释重力的理论。但是他拒绝了这个模型,因为模型中有大量未使用的超凡小体。约翰·普莱费尔(John Playfair)如此描述博什科维奇的论证:
| “ | 巨量的粒子,因此注定在无穷空间中继续他们永不完结的旅程,既不改变方向,也不回到它们的来处,这种假设几乎不为自然通常的俭省所支持。这无数洪流的动力从何而来?肯定是需要某种创造性力量的永恒努力,而这种力量又得在幅度和持续时间上无穷无尽吧?[16] | ” |
麦克斯韦后来提出了一个非常相似的论证(见下方小节)。另外,博什科维奇完全拒绝用接触力和瞬间推动力来解释重力,他认为引力是一种超距作用。
利希滕贝格、康德与谢林
[编辑]格奥尔格·克里斯托夫·利希滕贝格关于勒萨吉理论的知识[17]是依靠《牛顿式的卢克莱修》和普瑞弗斯特的一篇综述得来。利希滕贝格最早(像笛卡尔那样)相信自然现象的所有解释都必须要从直线运动和推动力而来,而勒萨吉的理论满足了这些条件。在 1790 年,他在一篇论文中表达对这一理论的热忱,相信勒萨吉的理论已怀有一切已知知识,使得在重力主题上的进一步幻想全无用处。他接着说:“如果这是一场梦,那么它是人所做过的最伟大而又雄壮的一场梦,我们能填上我们书卷中的漏洞,而这漏洞只能用梦来补上”。[18]
他在哥廷根大学的物理学讲座上经常援引勒萨吉理论。然而,在 1796 年利希滕贝格被伊曼努尔·康德的论证说服,因而改变了观点。康德批评了一切试图用推动力取代吸引力的理论。[19]康德指出,物质在空间上延展的一切构造,例如半径不为零的微粒,如果要存在,都必然要有某种结合力把其延展的各部分凝聚起来。这种力无法用重力微粒的推力来解释,因为这些微粒也必须以同样形式凝聚。为了避免这种循环论证,康德断定一定存在某种基本的吸引力。这种驳斥正是一世纪前对笛卡尔推动力学说的驳斥,而它甚至让笛卡尔的追随者都放弃其哲学理论的这一方面。
另外一位德国哲学家弗里德里希·谢林也驳斥了勒萨吉的模型,因为它的机械唯物论和谢林的唯心论、反唯物论哲学不相容。[20]
拉普拉斯
[编辑]皮耶-西蒙·拉普拉斯试图得到合乎天文观察的引力的速度时,部分参考了勒萨吉的理论。他计算出其速度必须“至少是光速的一亿倍”,才能够避免重力传播延迟使观测到的月球轨道有太大的畸变。[21]包括拉普拉斯在内的多数研究者都以此支持牛顿的超距瞬时作用观念,并且认为任何类似勒萨吉理论的模型都不可信。拉普拉斯同时论证要维持重力和质量成正比,地球的分子表面积最多是其可见表面积的千万分之一。拉普拉斯从未在其成果中直接提及勒萨吉的理论,这让勒萨吉很失望。
动力论
[编辑]因法蒂奥,克拉默与雷德克的理论都不甚为人所知,在 19 世纪下半叶,随气体动力论的发展,勒萨吉的阐述使得对该理论的兴趣重燃。
勒雷
[编辑]为了产生净重力,勒萨吉的微粒必定在与一般物体碰撞时失去速度,因此会有大量能量转换成内能。如果微粒的运动模式不存储内能,则这些能量只能由一般物体所吸收。对该问题,让·勒雷(Armand Jean Leray)[22]提出了一种微粒模型(与勒萨吉的模型十分相似),断定吸收来的能量被物体用于产生磁性和热。他认为这可能是星辰向外发散的能量的来源。
开尔文与泰特
[编辑]
勒萨吉自己的理论在十九世纪下半叶成为重燃兴趣的主题,是因为开尔文在 1873 年出版的论文。[23]和勒雷不同,他精确地处理了热的问题,并认为吸收来的能量将会极高,能在几分之一秒内就蒸发一切物体。因此,开尔文重复了法蒂奥曾在 1690 年代提出的观念,来试图解决勒萨吉理论固有的热力学问题。他认为这些过量的热必须被微粒本身吸收,并推测重力物质有涡旋的本性。换言之,微粒原先平移产生的动能必须转化成不同的运动模式(主要是振动和转动)来存储内能。借助鲁道夫·克劳修斯的推论——气体分子在任何特定运动模式下的能量与其总能量的比值趋于固定——开尔文接着认为因此蓄能但运动速度更慢的微粒会由于(在宇宙学尺度上)跟其他微粒的碰撞回复原先的运动状态。开尔文还断言可以从超凡小体流中汲取无穷的自由能,并描述了一个可以做到这点的永动机。
随后,彼得·格斯利·泰特认为勒萨吉理论是当时已提出的所有重力解释中唯一可信者。他接着说:
| “ | 该理论最奇特之处在于,假使它是真的,我们有可能推导出一切种类能量最终都是动能。[24] | ” |
开尔文自己对勒萨吉理论最终能得到对现象的完整描述一事并不乐观。在前述的 1873 年出版的扼要的论文后,他再也没有重返这个主题,除了下述的一段评论[25]:
| “ | 这种物质的动力学理论只是一个梦,除非它能解释化学亲和力、电、磁、重力、以及聚集涡旋的惯性。勒萨吉的理论可能给我们对重力的解释,及其在原子涡理论下,与物体惯性的关系——如果这不是来自晶体结构必然有的各向异性,加上重力似乎完美的各向同性的话。但没有任何已被发现的、或者可以想象的路标指出可能翻越这种困难、或者可能扭转其缺陷的道路。[26] | ” |
普雷斯顿
[编辑]萨缪尔·托尔弗·普雷斯顿(Samuel Tolver Preston)[27] 阐明勒萨吉对重力微粒做的许多假设(例如直线运动,极少相互碰撞,等等)可以被统一在同一个观念下,即它们(在宇宙学尺度上)类似拥有极长平均自由程的气体分子。普雷斯顿也接受了开尔文对微粒具有的储存内能的运动模式的假定。他用如下的例子说明开尔文的模型:用一个钢铁环与铁砧碰撞时,铁砧不会有太大的震动,但是钢环却会振动,并以衰减的速度离开。他同时认为,微粒的平均自由程至少是行星之间的距离——在更长的距离上,粒子就会由于碰撞重新得到其平移能量,因此他下结论在这么长的距离上物体之间不会有吸引力,和微粒的大小无关。
保罗·德鲁德(Paul Drude)认为这可能可以和卡尔·诺依曼(Carl Gottfried Neumann)与胡戈·冯·泽利格(Hugo von Seeliger)两人的理论链接,他们假定重力在开放空间中会在某种意义上被吸收。[28]
麦克斯韦
[编辑]
詹姆斯·克拉克·麦克斯韦于 1875 年,在第九版《大英百科全书》的〈原子〉条目下综述了开尔文—勒萨吉理论[29]。在描述该理论的基本概念后他写道(据 Aronson 所言,是种讽刺[30]):
| “ | 此处所呈现的似乎就是一条通向解释重力律则的道路,若能证明它在其他方面与事实一致,那它也许就会成为通往科学奥秘的皇家之路。[29] | ” |
麦克斯韦评论了开尔文对微粒有不同能量模式的见解,认为这蕴含重力微粒并不是简单的原始物质,而是一种有结构的系统,它自己内部仍有储存内能的运动模式,而这结构必须要由(未被解释的)吸引力来维持。他认为物体的温度,即物体分子的平均动能,必然趋近于超凡小体的平均动能,因此,由于后者远远大于前者,他作结认定普通物体应该在勒萨吉微粒的轰炸下,在几秒钟内焚烧殆尽。[29] 他写道:
| “ | 我们为该理论投入的空间似乎比它应得的更多,这是因为它很巧妙,并且因为它是迄今为止对引力起源的唯一一种可以被攻击和捍卫的理论。[29] | ” |
麦克斯韦还认为,该理论要求“消耗大量外力”,因此违反了作为自然基本原理的能量守恒。[29] 普雷斯顿对麦克斯韦的批评作出了回应,他认为如果微粒的质量足够小(并且数量密度足够大),就可以任意降低每个单个简单颗粒的动能。但是后来庞加莱对这个问题进行了更详细的讨论,他表明勒萨吉模型中的热力学问题仍然没有解决。
艾森卡赫、李沙尼克和杜博依斯-雷蒙
[编辑]卡斯帕·艾森卡赫(Caspar Isenkrahe)于 1879 到 1915 年间在多份出版物中描述自己的模型。[31]他的基本预设非常接近勒萨吉和普雷斯顿,但他更加详细描述了这种动力学的应用。但是,断言小体在碰撞后的速度减少却没有任何物体的能量上升,这让他的模型违反能量守恒定律。他注意到物体的重量和密度之间有关联(因为如果物体密度下降,那么物体内部的重力遮蔽就会减少),因此他断定温热的物体应该比冷的物体更重(和热胀冷缩效应相关)。
1887 年,阿达伯特·李沙尼克(Adalbert Ryšánek)的另一个模型[32]也做了仔细的分析,并运用了麦克斯韦的气体速度分布律。他还区分开重力介质和以太。这是有必要的,因为根据他的计算,如果重力介质同时是光行进的介质,则海王星轨道没有拖拽效应(即受到微粒介质的阻力)意味着微粒速度最少要是 5 · 1019 cm/s。他(类似勒雷)认为吸收的能量会转化成热,而这些热可能转移入以太,或者供恒星维持能量放出。但是,这些定性推论并没有被任何关于实际产热量的定量估计支持。
1888 年,保罗·杜博依斯-雷蒙(Paul du Bois-Reymond)驳斥勒萨吉的理论,部分由于勒萨吉理论预测的重力并非严格与质量成正比。为像在牛顿理论中那样得到精确的质量正比律(这意味着没有遮蔽或饱和作用,而物质的结构多孔且无限稀疏),超凡小体流必须无限强。杜博伊斯-雷蒙认为这很荒谬。另外,他像康德一样注意到勒萨吉理论无法达成其目标,因为他使用“弹性”或者“绝对坚硬”等概念,而这(在他看来)只能由超距吸引力解释。同样的问题也发生在对分子的结合力的解释上。因此,他认为这种理论的根本意图,即抛弃掉作为超距吸引力的基本力,是无法达到的。[33]
波模型
[编辑]凯勒与德布瓦博德兰
[编辑]1863 年,法兰索瓦·安东尼·爱德华·凯勒(François Antoine Edouard Keller)与 Em. 凯勒(Em. Keller)[34]提出把勒萨吉式力学和以太纵波结合在一起的理论。他们假设这些波在各个方向传播,并且当撞击物体时就减少一些动量,因此波在物体间造成的压力就会比在物体周围造成的压力来得小。1869 年,保罗·埃米尔·勒科克·德布瓦博德兰(Paul-Emile Lecoq de Boisbaudran)[35]提出和勒雷相同的理论(包括热的生产和吸收),但类似凯勒氏,他也把微粒换成以太纵波。
洛伦兹
[编辑]
在上述尝试后,二十世纪早期的其他作者也试图把勒萨吉的微粒替换成电磁辐射。这和当时的洛伦兹以太理论(Lorentz ether theory)和电子理论相关,它们假定物质有带电的结构。
1900 年,亨德里克·洛伦兹[36]认为勒萨吉的微粒模型和当时的电子理论不兼容。但后来发现电磁波列可以产生一些压力,而且伦琴射线(现在称为X射线)具有强大的穿透力,让他认定没有什么可以反对可能存在比X射线更有穿透力的辐射,这种辐射可以替代勒萨吉的微粒。洛伦兹证明带电粒子之间的吸引力确实可能存在(这种带电粒子可能用于物质基本亚单元的模型),但只有在入射能量完全被吸收的时候才会发生。该问题也是微粒模型面对的基本问题,因此洛伦兹写道:
| “ | 然而,情况是这样:这种吸引力只有在电磁能量以某种方式不断消失的情况下才可能存在,这种情况极为难见,以至于已述的不能说解释了引力。这也不是唯一可以提出的反对意见。如果万有引力的机制是以光速行进的穿越以太的振动,那么与天文学观测容许的程度相比,引力应该会对天体运动产生更大的影响。 | ” |
1922 年[37] ,洛伦兹首先检视了马丁·克努森(Martin Knudsen)的稀有气体研究,并将此与他对勒萨吉微粒模型的讨论联结在一起,随后总结了他自己的电磁勒萨吉模型——但他重复了他 1900 年的结论:没有吸收就没有重力效应。
在 1913 年大卫·希尔伯特援引并批评了洛伦兹的理论。他论证如果两个原子的距离相对重力电磁波长而言足够大,就不可能有形如 1/r2 的力产生。[38]
约瑟夫·汤姆森
[编辑]1904 年,约瑟夫·汤姆森[39]也考虑了一种勒萨吉式的模型,其中原始的超凡流是以一种假设性的、比X射线更有穿透力的辐射形式存在。他认为麦克斯韦的热问题可以避免,只要假定吸收来的能量不是转化成热,而是重新辐射出依然具备高穿透性的辐射流。他注意到这个过程可能可以解释放射性物质的能量从何而来——然而,他也表明放射性的来源更可能是物质内部。1911 年汤姆森在大英百科全书第十一版中名为“物质”的条目[40] 下回到该主题。他在该文说,这种二次辐射的形式有点类似于带电粒子穿过物质的过程如何引起甚至更具有穿透的X射线的辐射。他说:
| “ | 最近发现的一个非常有趣的结果是,勒萨吉为其理论目的引入的机械过程,与我们现在有直接的实验证据验证的事物非常相似。……然而,就我们所知,伦琴射线在被吸收时并没有产生更具穿透力的伦琴射线——要用它们解释吸引力,这应该要发生——但会产生穿透力较小的射线或同类的射线。[40] | ” |
托马西纳与布拉什
[编辑]和洛伦兹或者汤姆森不同,汤玛斯·托马西纳(Thomas Tommasina)[41]于 1903 到 1928 年间认为长波长辐射可以解释重力,而短波长辐射则用来解释物质凝聚力。查尔斯·布拉什[42]在 1911 年也假定长波长辐射可以解释重力。但他后来改变了他的观点并用极短波长辐射取代之。
晚近评估
[编辑]达尔文
[编辑]1905年,乔治·达尔文(George Darwin)计算了两个物体在非常近距离时,其间的重力,以确定几何效应是否会导致牛顿定律被违反。[43] 在这里,达尔文用尺寸均一的微观硬球体代替了勒萨奇的笼状物质结构。他的结论是只有在完全非弹性碰撞(零反射)的情况下,牛顿定律才会严格成立,这加强了勒萨吉理论的热力学问题。同样,只有在冲击的法向分量和切向分量都完全无弹性(与勒萨吉的散射机制相反)且物质基本粒子的大小完全相同时,这种理论才有效。他接着推论,辐射光的物体之间的推力,和完全吸收勒萨吉微粒造成的效果是可相互类比的。而表面温度不同的物体的各个部分将朝着较冷的部分移动。在后来对引力理论的综述中,达尔文简要描述了勒萨吉的理论,并说他认真考虑了该理论,但随后写道:
| “ | 我不会进一步提及这个概念,只能说我相信没有任何科学人愿意承认它提供了真正的道路。[44] | ” |
庞加莱
[编辑]
部分基于达尔文的计算,亨利·庞加莱在 1908 年对勒萨吉理论提出了重要的批评。[45]他认定理论产生的吸引力正比于, 其中 S 是地球表面的分子的总面积,v 是重力微粒的速度,ρ 是微粒介质的密度。与拉普拉斯一样,他论证要维持重力和质量成正比,S 最多只能是地球可见表面积的千万分之一。而微粒带来的拖拽效应(即微粒介质带来的阻力)正比于 Sρv,因此拖拽效应与引力的比反比于Sv。要减小拖拽效应,庞加莱认为 v 最少必须是光速的 24 · 1017 倍。现在有了 Sv 和 v 的最小容许值,和 S 的最大容许值,就可以算出产生的热,它正比于 Sρv3。该计算表明地球的温度将每秒上升 1026 度。庞加莱因此注意到“地球不能长期忍受这样的辖制”。庞加莱也分析了一些波模型(托马西纳与洛伦兹的),认为它们和微粒模型有同样的问题。为减少拖拽效应,波的速度同样必须超光速,也同样会有热问题。在描述和汤姆森类似的再辐射模型后,他下结论道:“这就是我们试图使勒萨奇的理论站得住脚时,被引导著做出的复杂假设。”
他还指出,如果在洛伦兹模型中将吸收的能量完全转换为热量,则每秒将使地球温度升高 1013 度。庞加莱接着在 19 世纪末和 20 世纪初发展出的“新动力学”的背景下继续研究勒萨吉的理论,特别考虑到了相对论原理。对于微粒理论,他指出“很难想像与相对性原理相容的碰撞定律”,并且仍然存在阻力和发热问题。
预测与批评
[编辑]物质和微粒
[编辑]物质的稀疏性
[编辑]该理论的基本预测是物质会极端稀疏。正如法蒂奥和勒萨吉在 1690/1758 年(以及之前的惠更斯)所假设的那样,物质的主要组成必须是空白空间,这样微粒才能几乎不受干扰地穿透物体,使物体的每一部分都可以参与引力相互作用。一段时间后,该预测(在某些方面上)获得证实。物质的确主要由空白空间组成,某些粒子(如中微子)几乎可以不受阻碍地穿过物质。但是,基本粒子作为经典实体的图景——靠直接碰撞来进行相互作用,而其作用情况取决于它们的形状和大小(例如法蒂奥/勒萨吉提出的网格结构以及艾森卡赫/达尔文的均一球体)——与当前对基本粒子的理解不一致。洛伦兹/汤姆森将带电粒子作为物质基本成分的建议也与当前的物理学相矛盾。
宇宙辐射
[编辑]每个勒萨吉式的模型都假设存在一个具有巨大强度和穿透力的、充满空间的各向同性微粒流或辐射。这与 20 世纪发现的宇宙微波背景辐射(CMBR)有一些相似之处。 CMBR 确实是一个充满空间且各向同性的辐射流,但是它的强度和穿透能力都非常小。来自(例如)太阳的中微子流具有勒萨吉为其超平凡小体所设想的穿透性,但这种粒子流却又不是各向同性的(因为个别恒星是中微子的主要来源),强度甚至更低于 CMBR。当然,CMBR 和中微子都不会以超光速传播,但这却是勒萨吉粒子的另一个必要属性。理察·费曼曾从更现代的角度来考虑,摒弃勒萨吉简单的“推力”概念,中微子(或其他类似中微子的粒子)也许可能是引力的量子场论中的中介粒子,但随后该想法又被他自己驳斥。[46]
重力遮蔽
[编辑]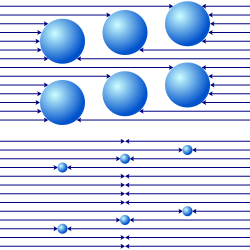
尽管在法蒂奥—勒萨吉理论中一般假设物质非常稀疏,但物质不会完全可被穿透,否则就不存在引力。但是,这会带来问题:如果物体的质量足够大,两块物体产生的阴影量,将由于阴影重叠,而少于它们各自阴影产生的阴影总和(图 10,上半)。这种称为重力屏蔽的假想效果意味着在添加物体时,重力的增幅不会与质量成正比。因此,为了保持理论设想可行,法蒂奥和勒萨吉都假设屏蔽效果小到无法被检测,换言之,要求物质相互作用的截面必须非常小(图 10,下半)。但为了要得到我们实际观测到的重力大小,这意味着引力流的最小强度也必须非常高。任何形式的引力屏蔽都将违反等效原理,并且与厄缶实验(Eötvös experiment)及其后续实验中观察到的极其精确的零结果(null result)不一致——所有这些结果都证实了广义相对论的预测,即主动引力质量、被动引力质量和惯性质量完全相等。[47]有关引力屏蔽与勒萨吉引力之间关系的更多历史信息,请参阅 Martins 的文章[48][49]和 Borzeszkowski 等人的文章[50]。
由于艾森卡赫关于密度、温度和重量之间关系的论断完全基于预测材料密度变化产生的影响,并且同一密度的物体可以升温也可以降温,因此艾森卡赫的评论并不能推导出温度和重力之间的任何基本关系。(实际上,温度和引力之间、原子结合能和引力之间确实存在关系,但是它们的实际效应与艾森卡赫的推测无关。请参见下面的“结合能”一小节。)至于对引力和物体密度有关的预测,所有实验证据都指示不存在这种关系。
重力的速度
[编辑]拖拽效应
[编辑]根据勒萨吉的理论,如果孤立的物体相对于超凡小体流的各向同性参考系(即在各个方向上超凡微粒的速度均相同的参考系)运动,则它会受到拖拽阻力的作用。这是由于以下事实:如果物体处于运动状态,则从前面撞击物体的微粒(相对于物体而言)要比从后面撞击物体的微粒速度更高——这种作用将减小太阳和地球的距离。该拖拽阻力的大小与 vu 成正比,其中 v 是粒子的速度,u 是物体的速度,而重力则与 v2 成正比,因此阻力与重力的比值与 u/v 成正比。因此,对于给定的重力强度,可以通过增加超凡小体的速度 v 来任意减小给定速度 u 下的阻力。然而,为了将阻力减小到经典力学上可接受的水平(即与观察结果一致),速度 v 必须比光速大许多个数量级。这使得勒萨吉理论与基于狭义相对论的现代力学从根本上不相容,因为根据后者,任何粒子(或波)都不能超过光速。另外,即使有可能是超光速微粒,这种微粒流的有效温度也足以在短短的几分之一秒内焚烧所有一般物质。
轨道畸变
[编辑]如拉普拉斯所证明的,另一种在勒萨吉模型中可能由于有限引力速度引起的效应是轨道的畸变(aberration)。除非勒萨吉微粒以远大于光速的速度运动——像勒萨吉或开尔文所认为的那样——否则物体之间的相互作用会存在时间延迟(即存在非零的传输时间)。在轨道运动的情况下,这会导致物体对另一个物体一段时间前的位置做出反应,从而对另一个物体产生一个切向力分量。与拖拽效应相反,这一分力将使两个对象加速相互远离。为了保持稳定的轨道,引力的作用必须比光速快得多,或引力并非纯粹的中心力。许多人认为这是对任何勒萨吉式理论的决定性驳斥。相反,广义相对论与拉普拉斯未观察到明显像差的结果一致,因为即使重力仅以光速传播,在广义相对论下,预期的轨道畸变也几乎完全被相互作用中与速度有关的项所抵消。[51]
重力的范围
[编辑]在许多微粒模型中,例如开尔文的微粒模型中,由于微粒之间相互作用的性质,重力的范围会受到限制。在这些模型中,微粒通过物质而产生的动量亏损(遮蔽)会转变为模型假定的其他运动模式,而这种运动模式又会使微粒相互碰撞时回复其原来的动量(使得遮蔽的阴影“模糊”),故重力的范围会取决于这种碰撞的速率,或者在有效意义上取决于微粒的平均自由程。也因此,在这些模型中关于重力有效范围的预测将有所变化,取决于对粒子相互作用可能模式的特定方面和其他特殊假设。但是,对于这类模型,已观察到的宇宙大尺度结构,例如银河系,表明重力的有效范围至少要有数百万光年,否则无法容许这些结构存在。这是对这种粒子散射模型的限制。
能量
[编辑]吸收
[编辑]如历史部分所述,所有勒萨吉式模型的共同主要问题是能量和热的问题。正如麦克斯韦和庞加莱所表明的,非弹性碰撞会导致物质在几分之一秒内蒸发,而已提出的解决方案并不令人信服。例如,Aronson[30] 给麦克斯韦的断言做了更简单的证明:
| “ | 假设与麦克斯韦的预设相反,物质分子实际上比粒子具有更多的能量。在这种情况下,粒子平均来说会在碰撞中获得能量,而被另一物体 B 拦截的粒子,将被从物体 B 反弹的更具能量的粒子所代替。如此一来,重力的作用将被逆转:与观察相反,物体之间将会产生斥力。另一方面,如果粒子和分子的平均动能相同,则不会发生净能量转移,并且碰撞将等同于弹性碰撞,这时正如已经证明的那样,不会产生引力。 | ” |
同样,艾森卡赫违反能量守恒定律也是不可接受的,开尔文对克劳修斯定理的应用则(如开尔文本人所指出的)造成了某种永动机,也违反了能量守恒定律。波模型的二次再辐射机制引起了汤姆森的兴趣,但是麦克斯韦或庞加莱并没有非常重视,因为它严重违反了热力学第二定律(大量能量自发地被吸收了,从较冷的形式转换为较热的形式),而这是所有物理定律中最牢固的一种。
这一能量问题也被膨胀地球说的支持者考虑,和他们认为存在质量吸积的观念相连(即地球通过引力吸引积累周围物质而膨胀)。早期将膨胀地球说与某种形式的推力重力下质量增加联结在一起的理论家包括亚尔科夫斯基(Ivan Osipovich Yarkovsky)与希尔根贝格(Ott Christoph Hilgenberg)[52]。主流科学家已不再认为质量吸积或膨胀地球说的观念是有效的,其中一个理由是根据质能等价原理,如果地球吸收超凡小体流的能量来产生我们观察到的引力(使用庞加莱计算的能量值),则其质量将会在几分之一秒内倍增。
原子结合能
[编辑]根据观察证据,现在知道重力与所有形式的能量相互作用,而不仅仅是与质量相互作用。原子核的静电结合能,原子核中弱相互作用的能以及原子中电子的动能都对原子的引力质量有贡献,这已在厄缶型实验中以高精确度得到证实。[53]这同时意味着一定数量的气体的原子运动得更快时,该气体的引力会增加。此外,月球镭射测距实验表明,甚至引力结合能本身也具有引力,其强度与等效原理的预测以高精确度一致——进一步证明,任何成功的引力理论都必须是非线性的,而且具有自耦合性。[54] [55]勒萨吉的理论没有预测上述影响的任何一部分,其理论的任何已知变体也都没有预测。
重力以外的应用与类比
[编辑]仿重力
[编辑]莱曼·史匹哲(Lyman Spitzer)在 1941 年[56]计算得出两个尘埃粒子吸收彼此之间的辐射会导致与 1/r2 成正比的净吸引力(显然他没有意识到了勒萨吉式的遮蔽机制,也没有注意到洛伦兹将辐射压力和重力类比的考虑) 。乔治·伽莫夫(George Gamow)将此效应称为“仿重力”。他于1949年提出[57]在大霹雳之后,电子的降温速度可能快于背景辐射的降温速度,而电子间辐射的吸收会导致勒萨吉式机制,这可能在大霹雳后不久的星系形成过程中发挥重要作用。然而,该猜测在 1971 年被 Field 否决了,[58]他表明这种影响太小,因为电子和辐射实际上几乎处于热平衡状态。1986 年,Hogan 和 White 认为[59] ,仿重力可能通过吸收星系形成前的星光影响了星系的形成。但 Wang 和 Field 又证明[60]任何形式的模拟引力都无法产生足够的力来影响星系的形成。
等离子体
[编辑]勒萨吉式机制也被认为是粉尘等离子体(dusty plasma)行为的重要因素。A.M. Ignatov[61] 证明了,由于等离子和尘埃离子之间的非弹性碰撞,在各向同性无碰撞等离子体中悬浮的两个尘埃颗粒间会产生吸引力。该吸引力与尘粒间距离的平方成反比,并且可以抵消尘粒间的库仑排斥力。
真空能
[编辑]在量子场论中,假定有所谓的虚粒子的存在,这导致了所谓的卡西米尔效应。卡西米尔计算得出,在计算真空能量时,仅应计数两块板之间具有特定波长的颗粒。因此,如果板彼此靠近,则板之间的能量密度就较小,从而导致板之间的净吸引力。但是,这种效应的概念框架与法蒂奥和勒萨吉的理论截然不同。
晚近发展
[编辑]勒萨吉理论在 19 世纪得到的重新评估发现了与该理论紧密相关的几个问题,包括过度加热、拖拽阻力、重力屏蔽和轨道畸变。对这些问题的认识,以及注意力从重力的机械解释普遍移走,导致人们对勒萨吉理论的兴趣逐渐丧失。最终在 20 世纪,爱因斯坦的广义相对论使勒萨吉的理论黯然失色。
1965 年,理察·费曼(Richard Feynman)检视了法蒂奥—勒萨吉机制,主要是把它当做范例,说明如何不用复杂数学,用较简单的操作来解释“复杂的”物理定律(在这种情况下,是指牛顿的平方反比定律),同时作为失败理论的示例。他指出,“弹跳粒子”的机制再现了平方反比定律,并且“奇异的数学关系大大减少”,但随后指出,该方案“不起作用”,因为它预言运动的物体会受到拖拽阻力。[62][63]
尽管它在主流科学界中被认为是不可行的理论,但偶尔也有人尝试在主流之外复兴该理论,包括 Radzievskii 与 Kagalnikova (1960),[64]Shneiderov (1961),[65]Buonomano 与 Engels (1976),[66]Adamut (1982),[67]Ioan-Iovitz Popescu (1982),[68]Jaakkola (1996),[69]Tom Van Flandern (1999),[70]Borge (2002),[71]Edwards (2007),[72]以及 Eid (2016)。[73]
Edwards 等人[74] 也讨论了各种勒萨吉模型和相关主题。
最近有一份有关新型定量推力理论的工作论文准备验证[75],该论文发表在CERN尚未引用的Zenodo平台上。
脚注
[编辑]- ^ 指用基本的简单机械过程来解释物理现象产生的理论。
- ^ Duillier, N. Fatio de, Lettre N° 2570, Société Hollandaise des Sciences (编), Oeuvres complètes de Christiaan Huygens 9, The Hague: 381–389, 1690a1888–1950 [2019-12-02], (原始内容存档于2020-11-16)
- ^ 3.0 3.1 3.2 见参考文献中的 Prévost (1805)。
- ^ Duillier, N. Fatio de, Die wiederaufgefundene Abhandlung von Fatio de Duillier: De la cause de la Pesanteur, Bopp, Karl (编), Drei Untersuchungen zur Geschichte der Mathematik, Schriften der Straßburger Wissenschaftlichen Gesellschaft in Heidelberg 10 (Berlin & Leipzig), 1701, 10: 19–661929
- ^ Duillier, N. Fatio de, Gagnebin, Bernard , 编, De la Cause de la Pesanteur: Mémoire de Nicolas Fatio de Duillier, Notes and Records of the Royal Society of London, 1743, 6 (2): 125–1601949, doi:10.1098/rsnr.1949.0018
|chapter=被忽略 (帮助)[永久失效链接] - ^ 6.0 6.1 6.2 6.3 Zehe (1980),见参考文献
- ^ Cramer, G., Theses Physico-Mathematicae de Gravitate (Dissertation), Geneva, 1731
- ^ Redeker, F. A., De cause gravitatis meditatio, Lemgoviae Ex Officina Meyeriana, 1736
- ^ “死力”是莱布尼兹用的词语,类似于今天所说的势能,与之相对的“活力”则类似于今天的动能。
- ^ Georges-Louis Le Sage, Letter à une académicien de Dijon.., Mercure de France, 1756: 153–171
- ^ Sage, G.-L. Le, Essai de Chymie Méchanique, Not published – private print, 1761 [2019-12-02], (原始内容存档于2020-12-05)
- ^ Sage, G.-L. Le, Lucrèce Newtonien, Memoires de l'Academie Royale des Sciences et Belles Lettres de Berlin, 1784: 404–432 [2020-06-01], (原始内容存档于2008-06-17),英文翻译可见于Sage, G.-L. Le, The Newtonian Lucretius, Langley, Samuel P. (编), The Le Sage theory of gravitation, Annual Report of the Board of Regents of the Smithsonian Institution, June 30, 1898: 139–160
- ^ Sage, G.-L. Le, Physique Mécanique des Georges-Louis Le Sage, Prévost, Pierre (编), Deux Traites de Physique Mécanique, Geneva & Paris: J.J. Paschoud: 1–186, 1818
- ^ Wolf (1852),见参考文献
- ^ Evanes (2002),见参考文献
- ^ Playfair (1807),见参考文献
- ^ Lichtenberg, G. C., Zehe, H.; Hinrichs, W. , 编, Aufzeichnungen über die Theorie der Schwere von G.L. Le Sage, Nachrichten der Akademie der Wissenschaften zu Göttingen, II. Mathematisch-physikalische Klasse (1), 2003, (1)
- ^ Lichtenberg, in German: "Ist es ein Traum, so ist es der größte und erhabenste der je ist geträumt worden, und womit wir eine Lücke in unseren Büchern ausfüllen können, die nur durch einen Traum ausgefüllt werden kann".
- ^ Kant, I., Metaphysische Anfangsgründe der Naturwissenschaft: Dynamik, Lehrsatz 5, 1786 [2019-12-02], (原始内容存档于2019-09-13)
- ^ Schelling, F.W.J., Ideen zu einer Philosophie der Natur (2. book, 3. chapter), 1797 [2019-12-02], (原始内容存档于2017-04-24)
- ^ Laplace, P.-S. 7. A Treatise in Celestial Mechanics 4. Chelsea, New York. 1966 [1805].
|issue=被忽略 (帮助) - ^ Leray, le P., Theorie nouvelle de la gravitation, Comptes Rendus, 1869, 69: 615–621 [2019-12-02], (原始内容存档于2020-01-25)
- ^ Thomson, William (Lord Kelvin), On the ultramundane corpuscles of Le Sage, Phil. Mag., 1873, 45: 321–332, doi:10.1080/14786447308640865
- ^ Tait, P. G., Lectures on some recent advances in physical science with a special lecture on force, London: Macmillan and Co., 1876, hdl:2027/mdp.39015064456968

- ^ 这一评论与开尔文自己相信的理论有关系,他认为原子是以太的涡旋。
- ^ Kelvin, Popular Lectures, vol. i. p. 145.
- ^ Preston, S. T., On some dynamical conditions applicable to LeSage's theory of gravitation, Phil. Mag., 5th Series, 1877, 4: 206–213 (pt. 1) and 364–375 (pt. 2), doi:10.1080/14786447708639322
- ^ Drude (1897),见参考文献
- ^ 29.0 29.1 29.2 29.3 29.4
 Maxwell, J. C., Atom, Baynes, T.S. (编), Encyclopædia Britannica 3 9th, New York: Charles Scribner's Sons: 38–47, 1878
Maxwell, J. C., Atom, Baynes, T.S. (编), Encyclopædia Britannica 3 9th, New York: Charles Scribner's Sons: 38–47, 1878
- ^ 30.0 30.1 (Aronson 1964),见参考文献
- ^ Isenkrahe, C., Das Räthsel von der Schwerkraft: Kritik der bisherigen Lösungen des Gravitationsproblems und Versuch einer neuen auf rein mechanischer Grundlage, Braunschweig: Friedrich Vieweg und Sohn, 1879
- ^ Ryšánek, A., Repert. Exp. Phys., 1887, 24: 90–115 缺少或
|title=为空 (帮助) - ^ Bois-Reymond, P. du, Ueber die Unbegreiflichkeit der Fernkraft, Naturwissenschaftliche Rundschau, 1888, 3 (14): 169–176
- ^ Keller, F.A.E; Keller, Ém., Mémoire sur la cause de la pesanteur et des effets attribués à l'attraction universelle, Comptes Rendus, 1863, 56: 530–533 [2019-12-02], (原始内容存档于2020-01-25)
- ^ Boisbaudran, Lecoq de, Note sur la théorie de la pesanteur, Comptes Rendus, 1869, 69: 703–705 [2019-12-02], (原始内容存档于2020-01-25)
- ^ Lorentz, H. A., Considerations on Gravitation, Proc. Acad. Amsterdam, 1900, 2: 559–574 [2019-12-02], (原始内容存档于2021-01-15)
- ^ Lorentz, H. A., Lectures On Theoretical Physics, London: Macmillan and Co., 1927 [1922]
- ^ Corry (1999),见参考文献
- ^ Thomson, J. J., Electricity and matter, Westminster: Archibald Constable & Co., Ltd., 1904
- ^ 40.0 40.1 Thomson, J. J. Matter. Chisholm, Hugh (编). Encyclopædia Britannica 17 (第11版). London: Cambridge University Press: 895. 1911.
- ^ Tommasina, T., La Physique de la Gravitation, Paris: Gauthier-Villars, 1928
- ^ Brush, C. F., A kinetic theory of gravitation, Nature, 1911, 86 (2160): 130–132, Bibcode:1911Natur..86..130., doi:10.1038/086130a0
- ^ Darwin, G. H., The analogy between Lesage's theory of gravitation and the repulsion of light, Proceedings of the Royal Society, 1905, 76 (511): 387–410 [2019-12-02], Bibcode:1905RSPSA..76..387D, doi:10.1098/rspa.1905.0042, (原始内容存档于2017-07-26)
- ^ Darwin, G. H., Introduction to Dynamical Astronomy, 1916
- ^ Poincaré, Henri, The Theory of Lesage, The foundations of science (Science and Method), New York: Science Press: 517–522, 1913
- ^ Feynman, R. P., Feynman Lectures on Gravitation, Addison-Wesley: 23–28, 1995
- ^ Bertolami, O; Paramos, J; et al. General Theory of Relativity: Will it survive the next decade?. 2006. arXiv:gr-qc/0602016
 .
.
- ^ Martin (1999),见参考文献
- ^ Martins (2002),见参考文献
- ^ Borzeskkowski et al. (2004),见参考文献
- ^ Carlip, S., Aberration and the Speed of Gravity, Phys. Lett. A, 2000, 267 (2–3): 81–87, Bibcode:2000PhLA..267...81C, arXiv:gr-qc/9909087
 , doi:10.1016/S0375-9601(00)00101-8
, doi:10.1016/S0375-9601(00)00101-8
- ^ Scalera, G.; Jacob, K.-H. (编), Why expanding Earth? – A book in honour of O.C. Hilgenberg, Rome: INGV, 2003
- ^ Carlip, S., Kinetic Energy and the Equivalence Principle, Am. J. Phys., 1998, 65 (5): 409–413, Bibcode:1998AmJPh..66..409C, arXiv:gr-qc/9909014
 , doi:10.1119/1.18885
, doi:10.1119/1.18885
- ^ Adelberger, E.G.; Heckel, B.R.; Smith, G.; Su, Y.; Swanson, H.E., Eötvös experiments, lunar ranging and the strong equivalence principle, Nature, Sep 20, 1990, 347 (6290): 261–263, Bibcode:1990Natur.347..261A, doi:10.1038/347261a0
- ^ Williams, J.G.; Newhall, X.X.; Dickey, J.O., Relativity parameters determined from lunar laser ranging, Phys. Rev. D, 1996, 53 (12): 6730–6739, Bibcode:1996PhRvD..53.6730W, doi:10.1103/PhysRevD.53.6730
- ^ Spitzer, L., The dynamics of the interstellar medium; II. Radiation pressure, The Astrophysical Journal, 1941, 94: 232–244, Bibcode:1941ApJ....94..232S, doi:10.1086/144328.
- ^ Gamow, George, On relativistic cosmogony, Reviews of Modern Physics, 1949, 21 (3): 367–373, Bibcode:1949RvMP...21..367G, doi:10.1103/RevModPhys.21.367.
- ^ Field, G. B., Instability and waves driven by radiation in interstellar space and in cosmological models, The Astrophysical Journal, 1971, 165: 29–40, Bibcode:1971ApJ...165...29F, doi:10.1086/150873.
- ^ Hogan, C.J., Mock gravity and cosmic structure, The Astrophysical Journal, 1989, 340: 1–10, Bibcode:1989ApJ...340....1H, doi:10.1086/167371.
- ^ Wang, B.; Field, G.B., Galaxy formation by mock gravity with dust?, The Astrophysical Journal, 1989, 346: 3–11, Bibcode:1989ApJ...346....3W, doi:10.1086/167981.
- ^ Ignatov, A.M., Lesage gravity in dusty plasma, Plasma Physics Reports, 1996, 22 (7): 585–589, Bibcode:1996PlPhR..22..585I
- ^ Feynman, R. P., The Character of Physical Law, The 1964 Messenger Lectures, Cambridge, Mass.: Massachusetts Institute of Technology: 37–39, 1967, ISBN 0-262-56003-8
- ^ Feynman's description of Le Sage's theory starts 7 minutes into this video clip (页面存档备份,存于互联网档案馆)
- ^ Radzievskii, V.V.; Kagalnikova, I.I., The nature of gravitation, Vsesoyuz. Astronom.-Geodezich. Obsch. Byull., 1960, 26 (33): 3–14 A rough English translation appeared in a U.S. government technical report: FTD TT64 323; TT 64 11801 (1964), Foreign Tech. Div., Air Force Systems Command, Wright-Patterson AFB, Ohio (reprinted in Pushing Gravity)
- ^ Shneiderov, A. J., On the internal temperature of the earth, Bollettino di Geofisica Teorica ed Applicata, 1961, 3: 137–159
- ^ Buonomano, V.; Engel, E., Some speculations on a causal unification of relativity, gravitation, and quantum mechanics, Int. J. Theor. Phys., 1976, 15 (3): 231–246, Bibcode:1976IJTP...15..231B, doi:10.1007/BF01807095
- ^ Adamut, I. A., The screen effect of the earth in the TETG. Theory of a screening experiment of a sample body at the equator using the earth as a screen, Nuovo Cimento C, 1982, 5 (2): 189–208, Bibcode:1982NCimC...5..189A, doi:10.1007/BF02509010
- ^ Popescu, I. I., Ether and Etherons. A Possible Reappraisal of the Concept of Ether, Romanian Academy Journal of Physics, 1982, 34: 451–468. Translation published as online edition (PDF), [2019-12-02], (原始内容存档 (PDF)于2016-01-13), Contemporary Literature Press, 2015. ISBN 978-606-760-009-4
- ^ Jaakkola, T., Action-at-a-distance and local action in gravitation: discussion and possible solution of the dilemma (PDF), Apeiron, 1996, 3 (3–4): 61–75 [2019-12-02], (原始内容存档 (PDF)于2019-10-24)
- ^ Flandern, T. Van, Dark Matter, Missing Planets and New Comets 2, Berkeley: North Atlantic Books: Chapters 2–4, 1999
- ^ Borge, C. J., Gravitação, teoria e prática – proposta do efeito ilha, São Paulo, Brazil.: Do Autor: 1–150, 2002, ISBN 8-590-26831-4
- ^ Edwards, M .R., Photon-Graviton Recycling as Cause of Gravitation (PDF), Apeiron, 2007, 14 (3): 214–233 [2019-12-02], (原始内容存档 (PDF)于2019-03-03)
- ^ Eid, C.O., Le Sage Push-Gravitation Revisited With Modern Knowledge of The Cosmic Background Radiation (PDF), Fundamental Journals, 2016 [2016-04-27], (原始内容 (PDF)存档于2018-06-03)
- ^ Edwards, M. R. (编), Pushing Gravity: New Perspectives on Le Sage's Theory of Gravitation, Montreal: C. Roy Keys Inc., 2002
- ^ Danilatos, G., Novel quantitative push gravity theory poised for verification, Zenodo, 2020 [2020-12-21], doi:10.5281/zenodo.4284106, (原始内容存档于2020-12-10)
参考文献
[编辑]- Aronson, S., The gravitational theory of Georges-Louis Le Sage, The Natural Philosopher, 1964, 3: 51–74 [2019-12-02], (原始内容存档于2006-03-05)
- Bellone, E., Classic and non-intentional consequences of some newtonian problems, Mem. Società Astronomica Italiana, 1991, 62 (3): 477–485, Bibcode:1991MmSAI..62..477B
- Borzeszkowski, H.-H.; Chrobok, T.; Treder, H.-J., G. T. Gillies; V. N. Melnikov; V. de Sabbata , 编, Screening and Absorption of Gravitation in Pre-Relativistic and Relativistic Theories, Proceedings of the 18th Course of the School on Cosmology and Gravitation, 2004: 1–37, Bibcode:2004grco.book....1V, ISBN 978-1-4020-1956-2, arXiv:gr-qc/0310081
 , doi:10.1007/978-1-4020-2242-5_1
, doi:10.1007/978-1-4020-2242-5_1 |contribution=被忽略 (帮助) - Chabot, H., Nombre et approximations dans la théorie de la gravitation de Lesage (PDF), Actes des Journées de Peirescq "La pensée numérique", Sciences et Techniques en Perspective, 2ème série, 2004, 8: 179–198 [2019-12-02], (原始内容 (PDF)存档于2017-04-24)
- Corry, L., David Hilbert between Mechanical and Electromagnetic Reductionism (PDF), Archive for History of Exact Sciences, 1999, 53 (6): 489–527 [2019-12-02], doi:10.1007/s004070050005, (原始内容存档 (PDF)于2020-09-25)
- Drude, Paul, Ueber Fernewirkungen, Annalen der Physik, 1897, 298 (12): I–XLIX [2019-12-02], Bibcode:1897AnP...298D...1D, doi:10.1002/andp.18972981220, (原始内容存档于2020-09-28)
- Evans, J. C., Gravity in the century of light: sources, construction and reception of Le Sage's theory of gravitation, Edwards, M.R. (编), Pushing Gravity: New Perspectives on Le Sage's Theory of Gravitation, Montreal: C. Roy Keys Inc.: 9–40, 2002
- Martins, de Andrade, R., The search for gravitational absorption in the early 20th century, Goemmer, H.; Renn, J.; Ritter, J. (编), The Expanding Worlds of General Relativity (Einstein Studies) 7, Boston: Birkhäuser: 3–44, 1999 [2019-12-02], (原始内容存档于2010-08-09)
- Martins, de Andrade, R., Gravitational absorption according to the hypotheses of Le Sage and Majorana, Edwards, M.R. (编), Pushing Gravity: New Perspectives on Le Sage's Theory of Gravitation (PDF), Montreal: C. Roy Keys Inc.: 239–258, 2002 [2019-12-02], (原始内容 (PDF)存档于2004-07-25)
- Playfair, J., Notice de la Vie et des Ecrits de George Louis Le Sage, Edinburgh Review, 1807: 137–153 English summary of Prévost (1805).
- Prévost, P. (编), Notice de la Vie et des Ecrits de George Louis Le Sage, Geneva & Paris: J.J. Paschoud, 1805 [2019-12-02], (原始内容存档于2007-11-12)
- Rowlinson, J. S., Le Sage's Essai de Chymie Méchanique, Notes Rec. R. Soc. Lond., 2003, 57 (1): 35–45, doi:10.1098/rsnr.2003.0195[永久失效链接]
- Taylor, W. B., Kinetic Theories of Gravitation, Annual Report of the Smithsonian Institution, 1876, 31: 205–282
- Wolf, R., George-Louis Le Sage, Biographien zur Kulturgeschichte der Schweiz (Orell, Füssli & co.), 1862, 4: 173–192 [2019-12-02], (原始内容存档于2012-11-11)
- Zehe, H., Die Gravitationstheorie des Nicolas Fatio de Duillier, Hildesheim: Gerstenberg, 1980, ISBN 3-8067-0862-2
- Zenneck, J., Gravitation, Encyklopädie der Mathematischen Wissenschaften mit Einschluss Ihrer Anwendungen (Leipzig), 1903, 5 (1): 25–67 [2019-12-02], ISBN 978-3-663-15445-7, doi:10.1007/978-3-663-16016-8_2, (原始内容存档于2021-03-12)

