三角形,又称三边形(英语: Triangle),是由三条线段顺次首尾相连,或不共线的三点两两连接,所组成的一个闭合的平面几何图形,是最基本和最少边的多边形。
一般用大写英语字母 、
、 和
和 为三角形的顶点标号;用小写英语字母
为三角形的顶点标号;用小写英语字母 、
、 和
和 表示边;用
表示边;用 、
、 和
和 给角标号,又或者以
给角标号,又或者以 这样的顶点标号来表示。
这样的顶点标号来表示。
锐角三角形的所有内角均为锐角。
钝角三角形是其中一角为钝角的三角形,其余两角均小于90°。
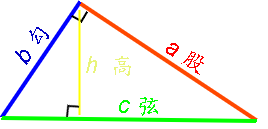
有一个角是直角(90°)的三角形为直角三角形。成直角的两条边称为“直角边”(cathetus),直角所对的边是“斜边”(hypotenuse);或最长的边称为“弦”,底部的一边称作“勾”(又作“句”),另一边称为“股”。斜边乘上斜边上的高÷2=勾股相乘÷2=此直角三角形面积(ch=ab)
直角三角形各边与角度的关系,可以三角比表示。
三条边边长皆不相等的三角形称为不等边三角形。
等边三角形(又称正三角形),为三边相等的三角形。其三个内角相等,均为60°。它是锐角三角形的一种。设其边长是  ,则其面积公式为
,则其面积公式为  。
。
等边三角形是正四面体、正八面体和正二十面体这三个正多面体面的形状。六个边长相同的等边三角形可以拼成一个正六边形。
对边是指一个角对面的那条边。比如∠A的对边就是BC,∠B的对边就是AC,∠C的对边就是AB。
对边测量是全站仪的一种专项测量功能,它可以间接测量两个不可通视点之间的水平距离。该方法设站灵活,操作简单,但它的测量精度没有标注,需要通过计算求得。
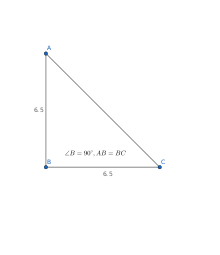 等腰直角三角形只有一种形状,其中两个角为45度。
等腰直角三角形只有一种形状,其中两个角为45度。
等腰三角形是三条边中有两条边相等(或是其中两只内角相等)的三角形。等腰三角形中的两条相等的边被称为“腰”,而另一条边被称为“底边”,两条腰交叉组成的那个点被称为“顶点”,它们组成的角被称为“顶角”。
等边三角形和等腰直角三角形是等腰三角形的特殊形式。
令其底边是  ,腰是
,腰是  ,则其面积公式为
,则其面积公式为  等腰三角形的对应高,角平分线和中线重合。
等腰三角形的对应高,角平分线和中线重合。
退化三角形是指面积为零的三角形。满足下列条件之一的三角形即可称为退化三角形:三个内角的度数为(180°,0°,0°)或(90°,90°,0°);三边其中一条边的长度为0;一条边的长度等于另外两条之和。有人认为退化三角形并不能算是三角形,这是由于它介乎于三角不等式之间,在一些资料中已否定了其中一条边等于其余两条边之和的情况。
勒洛三角形(英语:Reuleaux triangle),也译作莱洛三角形或弧三角形,又被称为划粉形或曲边三角形,是除了圆形以外,最简单易懂的勒洛多边形,一个定宽曲线。将一个曲线图放在两条平行线中间,使之与这两平行线相切,则可以做到:无论这个曲线图如何运动,只要它还是在这两条平行线内,就始终与这两条平行线相切。这个定义由十九世纪的德国工程师弗朗茨·勒洛命名。
- 三角边长不等式
- 三角形两边之和大于第三边,两边之差的绝对值小于第三边。如果两者相等,则是退化三角形。
- 三角内外角不等式
- 三角形任意一个外角大于不相邻的一个内角。

- 三角形外角
- 三角形两内角之和,等于第三角的外角。
- 三角形内角和
- 在欧几里德平面内,三角形的内角和等于180°。
毕氏定理,又称毕氏定理或毕达哥拉斯定理。其断言,若直角三角形的其中一边  为斜边,即
为斜边,即  的对角
的对角  ,则
,则
 。
。
毕氏定理的逆定理亦成立,即若三角形满足
 ,
,
则

设  为三角形外接圆半径,则
为三角形外接圆半径,则

对于任意三角形:



毕氏定理是本定理的特殊情况,即当角  时,
时,  ,于是
,于是  化简为
化简为  。
。
三角形具有稳定性,若二个三角形有以下的边角关系确定后,它的形状、大小就不会改变,二个三角形即为全等三角形。全等三角形的判断准则有以下几种:
- SSS(Side-Side-Side,边、边、边):各三角形的三条边的长度都对应地相等。
- SAS(Side-Angle-Side,边、角、边):各三角形的其中两条边的长度都对应地相等,且两条边夹着的角都对应地相等。
- ASA(Angle-Side-Angle,角、边、角):各三角形的其中两个角都对应地相等,且两个角夹着的边都对应地相等。
- RHS(Right Angle-Hypotenuse-Side,直角、斜边、边):在直角三角形中,斜边及一条直角边对应地相等。[1][注 1]
- AAS(Angle-Angle-Side,角、角、边):各三角形的其中两个角都对应地相等,且其中一组对应角的对边也对应地相等。
SSA(Side-Side-Angle、边、边、角)不能保证两个三角形全等,除非该角大于等于90°,此时可以保证全等。[2]:34[3]
- AA(Angle-Angle,角、角):各三角形的其中两个角的都对应地相等。(或称AAA(Angle-Angle-Angle,角、角、角))
- 三边成比例(3 sides proportional):各三角形的三条边的长度都成同一比例。
- 两边成比例且夹角相等(ratio of 2 sides, inc.∠):各三角形的两条边之长度都成同一比例,且两条边之夹角都对应地相等。(或称 2 sides proportional, inc. ∠ equal)
三角形中有着一些特殊线段,是三角形研究的重要对象。
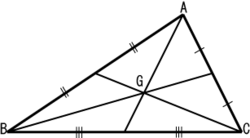
- 中线(median):三角形一边中点与这边所对顶点的连线段。
- 高线(altitude):从三角形一个顶点向它的对边所作的垂线段。
- 角平分线(angle bisector):平分三角形一角、一个端点在这一角的对边上的线段。
- 垂直平分线(perpendicular bisector):通过三角形一边中点与该边所垂直的线段,又称中垂线。
以上特殊线段,每个三角形均有三条,且三线共点。
设在 中,若三边
中,若三边 、
、 、
、 的中线分别为
的中线分别为 、
、 、
、 ,则:
,则:



设在 中,连接三个顶点
中,连接三个顶点 、
、 、
、 上的高分别记作
上的高分别记作 、
、 、
、 ,则:
,则:



其中  。
。
设在 中,若三个角
中,若三个角 、
、 、
、 的角平分线分别为
的角平分线分别为 、
、 、
、 ,则:
,则:



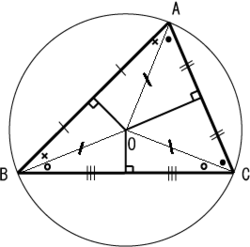
三角形的内心(Incenter) 、外心(Circumcenter)、垂心(Orthocenter) 及形心(Centroid)称为三角形的四心,定义如下:
关于三角形的四心,有这样的一首诗:
| “
|
内心全靠角平分,
外心中点垂线伸,
垂心垂直画三高,
形心角连线中心。
|
”
|

垂心(蓝)、形心(黄)和外心(绿)能连成一线,且成比例1:2,称为欧拉线,与九点圆的圆心(红)四点共线,为垂心和形心线段的中点。
连同以下的旁心,合称为三角形的五心:
设外接圆半径为 , 内切圆半径为
, 内切圆半径为 ,则:
,则:


其中 为三角形面积;
为三角形面积; 为三角形半周长,
为三角形半周长,
三角形的面积  是底边
是底边  与高
与高  乘积的一半,即:
乘积的一半,即:
 ,
,
其中的高是指底边与对角的垂直距离。
证明
 三角形的面积可表示为一长方形面积的一半。
三角形的面积可表示为一长方形面积的一半。
从右图可知,将两个全等三角形相拼,可得一平行四边形。而将该平行四边形分割填补,正好能得到一个面积等于  的长方形。因此原来的三角形面积为
的长方形。因此原来的三角形面积为
 。
。
证毕。
设 
 为已知的两边,
为已知的两边,  为该两边的夹角,则三角形面积是:
为该两边的夹角,则三角形面积是:
 。
。
证明
 三角形的高h能以正弦的定义表示。
三角形的高h能以正弦的定义表示。
观察右图,根据正弦的定义:
 。
。
因此:
 。
。
将此式代入基本公式,可得:
 。
。
证毕。
 、
、  为已知的两角,
为已知的两角,  为该两角的夹边,则三角形面积是:
为该两角的夹边,则三角形面积是:
 。
。
证明
 三角形的面积能从两角及其夹边求得。
三角形的面积能从两角及其夹边求得。
从正弦定理可知:

代入  ,得:
,得:
 。
。
注意到 ,因此:
,因此:
![{\displaystyle {\begin{aligned}A&={\frac {a^{2}\sin \beta \sin \gamma }{2\sin[180^{\circ }-(\beta +\gamma )]}}\\&={\frac {a^{2}\sin \beta \sin \gamma }{2\sin(\beta +\gamma )}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b89d1a8b04836b7ba80972fe0f1b3aedb7280e5)
证毕。
海伦公式,其表示形式为:
 ,
,
其中  等于三角形的半周长,即:
等于三角形的半周长,即:

秦九韶亦求过类似的公式,称为三斜求积法:
![{\displaystyle A={\sqrt {{\frac {1}{4}}{\left[c^{2}a^{2}-\left({\frac {c^{2}+a^{2}-b^{2}}{2}}\right)^{2}\right]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6f2fbc21365f1afa144d659370d9cb5869a12be)
也有用幂和来表示的公式:
 [注 2]
[注 2]
证明
将海伦公式略为变形,知
![{\displaystyle 16A^{2}=[(a+b)+c][(a+b)-c]\times [c+(a-b)][c-(a-b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7253baad63f0b4d87117038d3c2aa440ea007206)
多次使用平方差公式,得
![{\displaystyle {\begin{aligned}16A^{2}&=[(a+b)^{2}-c^{2}]\times [c^{2}-(a-b)^{2}]\\&=[2ab+(a^{2}+b^{2}-c^{2})]\times [2ab-(a^{2}+b^{2}-c^{2})]\\&=(2ab)^{2}-(a^{2}+b^{2}-c^{2})^{2}\\&=4a^{2}b^{2}-(a^{4}+b^{4}+c^{4}+2a^{2}b^{2}-2b^{2}c^{2}-2a^{2}c^{2})\\&=(2a^{2}b^{2}+2b^{2}c^{2}+2a^{2}c^{2})-(a^{4}+b^{4}+c^{4})\\&=2(a^{2}b^{2}+b^{2}c^{2}+a^{2}c^{2})-(a^{4}+b^{4}+c^{4})\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07a06b2e97f507877bd44020043ee18f60e83f3f)
等号两边开根号,再同除以4,得

亦可用Cayley–Menger行列式表示的公式:

基于海伦公式在三角形拥有非常小的角度时并不数值稳定,有一个变化的计法。设  ,三角形面积为:
,三角形面积为:
![{\displaystyle A={\frac {1}{4}}{\sqrt {[a+(b+c)][c-(a-b)][c+(a-b)][a+(b-c)]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e919b8f2964ae924ede8dc8eea803f9b496cdcf) 。
。
由  、
、  及
及  三个顶点构成的三角形,其面积可用行列式的绝对值表示:
三个顶点构成的三角形,其面积可用行列式的绝对值表示:

证明
无论三角形的顶点位置如何,该三角形总可以用一个直角梯形(或矩形)和两个直角三角形面积的和差来表示,而在直角坐标系中,已知直角梯形(或矩形)和直角三角形的顶点的坐标,该三角形的面积容易求出,即用上述的行列式表示。
若三个顶点设在三维坐标系上,即由  、
、  及
及  三个顶点构成三角形,其面积等于各自在主平面上投影面积的毕氏和,即:
三个顶点构成三角形,其面积等于各自在主平面上投影面积的毕氏和,即:

设三角形三边边长分别为  、
、  及
及  ,三角形半周长(
,三角形半周长(  )为
)为  ,内切圆半径为
,内切圆半径为  ,则:
,则:

若设外接圆半径为  ,则:
,则:

证明
内切圆半径公式
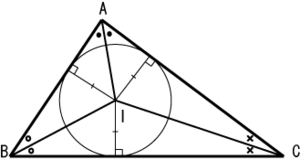 三角形被三条角平分线分成三分。
三角形被三条角平分线分成三分。
根据右图,设  ,
,  ,
,  ,则三角形面积可表示为:
,则三角形面积可表示为:

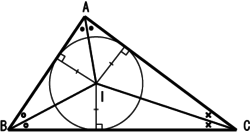
外接圆半径公式
根据正弦定理:

因此:

设从一角出发,引出两边的向量为  及
及  ,三角形的面积为:
,三角形的面积为:

证明
根据向量积定义, ,
其中
,
其中  是两支向量的夹角。
是两支向量的夹角。
因此:

证毕。
在三角形 中,三个角的半角的正切和三边有如下关系:
中,三个角的半角的正切和三边有如下关系:















































































![{\displaystyle {\begin{aligned}A&={\frac {a^{2}\sin \beta \sin \gamma }{2\sin[180^{\circ }-(\beta +\gamma )]}}\\&={\frac {a^{2}\sin \beta \sin \gamma }{2\sin(\beta +\gamma )}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b89d1a8b04836b7ba80972fe0f1b3aedb7280e5)

![{\displaystyle A={\sqrt {{\frac {1}{4}}{\left[c^{2}a^{2}-\left({\frac {c^{2}+a^{2}-b^{2}}{2}}\right)^{2}\right]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6f2fbc21365f1afa144d659370d9cb5869a12be)

![{\displaystyle 16A^{2}=[(a+b)+c][(a+b)-c]\times [c+(a-b)][c-(a-b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7253baad63f0b4d87117038d3c2aa440ea007206)
![{\displaystyle {\begin{aligned}16A^{2}&=[(a+b)^{2}-c^{2}]\times [c^{2}-(a-b)^{2}]\\&=[2ab+(a^{2}+b^{2}-c^{2})]\times [2ab-(a^{2}+b^{2}-c^{2})]\\&=(2ab)^{2}-(a^{2}+b^{2}-c^{2})^{2}\\&=4a^{2}b^{2}-(a^{4}+b^{4}+c^{4}+2a^{2}b^{2}-2b^{2}c^{2}-2a^{2}c^{2})\\&=(2a^{2}b^{2}+2b^{2}c^{2}+2a^{2}c^{2})-(a^{4}+b^{4}+c^{4})\\&=2(a^{2}b^{2}+b^{2}c^{2}+a^{2}c^{2})-(a^{4}+b^{4}+c^{4})\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07a06b2e97f507877bd44020043ee18f60e83f3f)



![{\displaystyle A={\frac {1}{4}}{\sqrt {[a+(b+c)][c-(a-b)][c+(a-b)][a+(b-c)]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e919b8f2964ae924ede8dc8eea803f9b496cdcf)








































