相似三角形
外觀
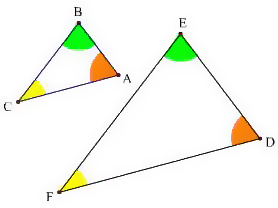
如圖,三個對應的內角的角度都一樣(但邊長大小無需一樣)的兩個三角形,或:對應角相等,對應邊成比例的兩個三角形稱為「相似三角形(similar triangles)」,其對應邊之比稱為相似比;兩個相似比為 1 的相似三角形稱為全等三角形。
- 下列三對邊長,稱為「對應邊」
- 下列三對角,稱為「對應角」
當兩個三角形相似時,我們利用下面的符號來表示:
- 利用上面的符號表示時,必須保持對應角的正確順序,不可隨意排列。
判定
[編輯]- 平行於三角形一邊的直線和其他兩邊相交,所構成的三角形與原三角形相似。
- 三邊成比例的兩個三角形相似。
- 兩邊成比例且夾角相等的兩個三角形相似。(注意:與全等類似,兩個三角形若兩邊成比例、且另一角(非夾角)相等,則並不一定相似。)
- 兩角分別相等的兩個三角形相似(AAA 或 AA)
- 如果兩個三角形分別與同一個三角形相似,那麼這兩個三角形也相似。
- 兩個直角三角形的斜邊、直角邊成比例則相似。
性質
[編輯]對應角相等
[編輯]若兩個三角形相似,則三個對應角相等。
若2個三角形相似,則三個對應邊長成比例。除此之外,兩三角形對應的中線、高、角平分線、周長均成比例,面積比是相似比的平方。
- 為兩個三角形的相似比。
- 相似三角形的對應角相等,對應邊成比例。
- 相似三角形對應高的比,對應中線的比和對應角平分線的比都等於相似比。
- 相似三角形周長的比等於相似比。
- 相似三角形的面積的比等於相似比的平方。





