线性分类器
在机器学习领域,分类的目标是指将具有相似特征的对象聚集。而一个线性分类器则透过特征的线性组合来做出分类决定,以达到此种目的。对象的特征通常被描述为特征值,而在向量中则描述为特征向量。
定义
[编辑]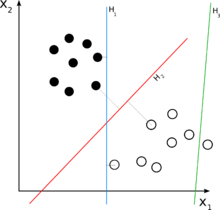
如果输入的特征向量是实数向量,则输出的分数为:
- ,
其中是一个权重向量,而f是一个函数,该函数可以通过预先定义的功能块,映射两个向量的点积,得到希望的输出。权重向量是从带标签的训练样本集合中所学到的。通常,"f"是个简单函数,会将超过一定阈值的值对应到第一类,其它的值对应到第二类。一个比较复杂的"f"则可能将某个东西归属于某一类。
对于一个二元分类问题,可以设想成是将一个线性分类利用超平面划分高维空间的情况: 在超平面一侧的所有点都被分类成"是",另一侧则分成"否"。
作为最快分类器,线性分类器通常应用于对分类速度有较高要求的情况下,特别是当为稀疏向量时。虽然如此,决策树可以更快。此外,当的维度很大时,线形分类器通常表现良好。如文本分类时,传统上,中的一个元素是文章所使用到的某个辞汇的出现的次数。在这种情况下,分类器应被适当地正则化。
生成模型与判别模型
[编辑]有两种类型用来决定[1][2]的线性分类器。第一种模型条件机率。这类的算法包括:
第二种方式则称为判别模型(discriminative models),这种方法是试图去最大化一个训练集(training set)的输出值。在训练的成本函数中有一个额外的项加入,可以容易地表示正则化。例子包含:
- Logit模型 --- 的最大似然估计,其假设观察到的训练集是由一个依赖于分类器的输出的二元模型所产生。
- 感知元(Perceptron) --- 一个试图去修正在训练集中遇到错误的算法。
- 支持向量机 --- 一个试图去最大化决策超平面和训练集中的样本间的边界(margin)的算法。
注意:相对于名字,线性判别分析在分类学并不属于判别模型这类。然而,当我们比较线性判别分析和另一主要的线性降维算法:主成分分析,它的名字则是有意义的。线性判别分析是一个监督式学习算法,会使用资料中的标签。而主成分分析是一个不考虑标签的非监督式学习算法。简而言之,这个名字是一个历史因素[3]。
判别训练通常会比模型化条件密度函数产生较高的准确。然而,在处理遗失资料时,使用条件密度模型通常是更为简单的。
所有以上所列线性分类器演算法,只要使用kernel trick都可被转成在另一个向量空间的非线性演算法。
另见
[编辑]参考文献
[编辑]引用
[编辑]- ^ T. Mitchell, Generative and Discriminative Classifiers: Naive Bayes and Logistic Regression. Draft Version, 2005 download (页面存档备份,存于互联网档案馆)
- ^ A. Y. Ng and M. I. Jordan. On Discriminative vs. Generative Classifiers: A comparison of logistic regression and Naive Bayes. in NIPS 14, 2002. download (页面存档备份,存于互联网档案馆)
- ^ R.O. Duda, P.E. Hart, and D.G. Stork. "Pattern Classification", Wiley, 2001. ISBN 0-471-05669-3, p. 117.
来源
[编辑]- Y. Yang, X. Liu, "A re-examination of text categorization", Proc. ACM SIGIR Conference, pp. 42-49,(1999). paper @ citeseer (页面存档备份,存于互联网档案馆)
- R. Herbrich, "Learning Kernel Classifiers: Theory and Algorithms," MIT Press,(2001). ISBN 0-262-08306-X





