约翰内斯·开普勒
| 约翰内斯·克卜勒 Johannes Kepler | |
|---|---|
 1627年的克卜勒 | |
| 出生 | 1571年12月27日 神圣罗马帝国魏尔代施塔特 |
| 逝世 | 1630年11月15日(58歲) 神聖羅馬帝國雷根斯堡 |
| 教育程度 | |
| 知名于 | |
| 科学生涯 | |
| 研究领域 | 天文學、占星术、数学及自然哲学 |
| 博士導師 | 麥可·梅斯特林 |
| 签名 | |
| 本条目所属系列 |
| 物理宇宙学 |
|---|
 |
约翰内斯·开普勒(德語:Johannes Kepler,德语:[joˈhanəs ˈkɛplɐ],1571年12月27日—1630年11月15日),德国天文學家、數學家。开普勒是十七世紀科學革命的關鍵人物。他最為人知的成就為开普勒定律,這是爾後天文學家根據他的著作《新天文学》、《世界的和諧》、《哥白尼天文学概要》萃取而成的三條定律。這些傑作對艾薩克·牛頓影響極大,啟發牛頓後來得出牛頓萬有引力定律。
开普勒曾在奥地利格拉茨的一家神学院担任数学教师,成为汉斯·乌尔里奇·艾根伯格亲王的同事。后来,他成了天文学家第谷·布拉赫的助手,并最终成为皇帝鲁道夫二世及其两任继任者马蒂亚斯和费迪南二世的皇家数学家。他还曾经在奥地利林茨担任过数学教师及华伦斯坦将军的顾问。此外,他在光学领域做了基础性的工作,发明了一种改进型的折光式望远镜(开普勒望远镜),并提及了同时期的伽利略利用望远镜得到的发现。
开普勒生活的年代,天文学与占星学没有清楚的区分,但是天文学(文科中数学的分支)与物理学(自然哲学的分支)却有着明显的区分。因為宗教信仰,开普勒將宗教論點和理由寫進他的作品。因為相信上帝用智慧創造世界,人只要透過自然理性之光,也可理解上帝創造的計畫。[1]。开普勒将他的新天文学描述为“天体物理学[2]”、“到亚里士多德的《形而上学》的旅行[3]”、“亚里士多德宇宙论的补充[4]”、通过将天文学作为通用数学物理学的一部分改变古代传统的物理宇宙学[5]。
早年
[编辑]

约翰内斯·开普勒于1571年12月27日,也就是当年的圣若望庆日,在帝国自由城魏尔德尔斯塔特(今德国巴登-符腾堡州的一部分,位于斯图加特市中心以西30km)出生,在他前面有两个哥哥和一个姐姐。他的祖父西博尔德·开普勒(Sebald K.)曾经是这个城镇的市长,但是约翰内斯·开普勒出生时,开普勒家族的家业已經开始衰落。他的父亲海因里希·开普勒(Heinrich K.)为了营生,当了一名危险的雇佣兵,在约翰内斯五岁的时候就离开了家庭,据说后来死于荷兰的“八十年战争”。约翰内斯的母亲凯瑟琳那·古尔登曼(K. Guldenmann)是一名旅店老板的女儿,同时是一名医生和草药商。约翰内斯是早产儿,孩提时体弱多病。然而,他超常的数学才能经常给他外祖父旅馆内的客人留下深刻的印象。[6]
他在很早的年纪就接触到并喜欢上了天文学,而这种喜欢贯穿了他的一生。在他6岁时,他看到了1577年的大彗星,并写道[7]他“被妈妈带到一处高地看彗星。”在他9岁时,他观察到了另外一次天文事件——1580年的月食,并记录道[7]他记得他被“叫到门外”看月食,月亮“看起来非常红”。然而,童年患上天花,使他的视力衰弱,双手残废,因此限制了他天文观察的能力[8]。
1589年,在经历过文法学校、拉丁学校以及毛尔布劳恩(Maulbronn)的神学院之后,开普勒进入了图宾根大学的图宾根神学院。在那里,他师从维塔斯·穆勒(Vitus Müller)学习哲学[9]及雅各布·黑尔布兰德(J. Heerbrand,菲利普·梅兰希< Philipp Melanchthon>在威登堡的学生)学习神学。雅各布·黑尔布兰德同时还教了另外一名当时还是学生的迈克尔·马斯特直至他在1590年成为图宾根校长[10]。他证实了自己是一名杰出的数学家,并作为一名熟练的占星家给同窗占星,为自己赢得了声誉。在1583-1631年间担任图宾根大学数学教授的迈克尔·马斯特林的教导下,他学习了关于行星运动的托勒密体系与哥白尼学说。在那段时间,他自己成了哥白尼的擁護者。在一次学生辩论中,他从理论和神学两个角度捍卫太阳中心说,坚称太阳是宇宙动力的主要来源[11]。虽然他很想成为一名牧师,在他学业将要结束之际,开普勒被推荐担任格拉茨新教学校(后来成为格拉茨大学)的数学与天文学教师。他于1594年4月接受了该职位,时年23岁[12]。
格拉茨(1594-1600年)
[编辑]《宇宙的神秘》
[编辑]
开普勒的第一部主要天文学作品——《宇宙的神秘》是第一部捍卫哥白尼学说、公开发表的作品。开普勒声称在格拉茨教学的1595年7月19日顿悟,在黄道十二宫图中展示了土星和木星的定期相遇:他意识到正多边体按照规定的比率与一个内切圆和外切圆相连,他推测这可能是宇宙的几何基础。在寻找符合已知的天文学发现(甚至使用加入该系统的额外星球)、独特排列的多面体的努力失败后,开普勒开始用立体的多面体进行实验。他发现五个柏拉图多面体中的每一个都可通过球体进行独特的内切和外切;先构建这些多面体,每一个多面体装在一个球体里,这个球体又装在另一个多面体内,每个多面体可产生6层,分别对应6个已知的星球——水星、金星、地球、火星、木星和土星。对这些多面体进行正确的排序——八面体、二十面体、十二面体、四面体和六面体,开普勒发现假设这些星球环绕着太阳,那么球体可以按照一定的间距进行排列,间距对应于每个星球路径的相对尺寸(在已知的天文学观测结果的精确度范围内)。开普勒还发现了一个公式,将每个星球的轨道大小与其轨道周期进行关联:从里星球到外星球,轨道周期的增长率是轨道半径差的两倍。然而,开普勒后来又否定了这个公式,因为这个公式不够精确。[13]

正如他在标题中所表明的,开普勒认为他已经揭示了上帝对宇宙的几何规划。开普勒对于哥白尼学说的许多热情源于他对于物质与精神之间的联系的神学信仰;宇宙本身是上帝的一个影像,太阳对应圣父,星球对应圣子,它们之间的间隔对应圣灵。《宇宙的神秘》的最初手稿包含了一延伸章节,用以调和太阳中心说与貌似支持地球中心说的圣经选段。[14]
在其老师迈克尔·马斯特林的支持下,开普勒获准在图宾根大学理事会发表他的手稿,期间他删掉了《圣经》注释,增加了对哥白尼学说及他的新想法更简单易懂的描述。《宇宙的神秘》于1596年年底发表,开普勒于1597年年初收到了发表的版本,并将其发送给著名的天文学家与赞助人。该书并未被广泛阅读,但是它建立了开普勒作为一名高水平的天文学家的声誉。对赞助人及格拉茨管理他职位的人充满热情的付出,也是他进入赞助体系的关键之路。[15]
开普勒从未放弃柏拉图式的多面体-球体宇宙学说——《宇宙的神秘》,虽然根据他后来的作品,其中的一些细节可能需要修改。他后来的主要作品,通过计算行星轨道的离心率,发现更精确的球体内外尺寸,但在某种意义上都是对该作品的进一步发展。1621年,开普勒发表了他扩展后的第二版《宇宙的神秘》,比第一版长一半,在脚注部分详细记录了在第一版发表之后的25年内他所作的修正与改进。[16]
关于其影响,《宇宙的神秘》可以视为将尼古拉斯·哥白尼在他的作品《天体运行论》中提出的理论进行现代化的重要的第一步。当哥白尼试图在该书中发展日心学说的时候,他用托勒密工具(即周转圆与离心圆)解释星球轨道速度的变化,并继续用地球轨道中心作为参考点,而不是用太阳中心“辅助计算以便使读者不会因偏离托勒密太多而感到混淆。”现代天文学家很大部分归功于《宇宙的神秘》,尽管它的主要论点有瑕疵,“因为它代表了清除哥白尼学说中托勒密理论残留的第一步。”[17]
与芭芭拉·穆勒的婚姻
[编辑]
1595年12月,开普勒被介绍给了芭芭拉·穆勒(B. Müller),一个带着幼小女儿——吉玛·德威纳维尔德(Gemma van Dvijneveldt)的23岁寡妇(结过两次婚),并开始向她求爱。穆勒不但是她前两任丈夫财产的女继承人,同时也是一名成功磨坊老板的女儿。尽管开普勒有着高贵的身份,但是她父亲约布斯特(Jobst)最初也反对他们的婚姻;虽然开普勒继承了他祖父的高贵身份,但是他的贫困使他与芭芭拉不般配。开普勒完成《宇宙的神秘》之后,约布斯特动了怜悯之心,但是这个婚约差点告吹,因为开普勒外出专注于出版的各项事宜。然而,帮忙建立该婚配的教会官员强迫穆勒遵守他们的协议。1597年4月27日,芭芭拉和开普勒结婚。[18]
在他们婚姻的早年,他们生育了两个子女(海因里希与苏珊娜),但是都在襁褓里夭折了。1602年,他们又生了一个女儿(苏珊娜),1604年,生了一个儿子(弗里德里希),1607年又生了一个儿子(路德维格)。[19]

其它研究
[编辑]《宇宙的神秘》出版之后,在格拉茨学校检察员的支持下,开普勒开始了他的雄心计划,进一步发展和完善他的作品。他计划编写另外4部书籍:一部关于宇宙的静止事物(太阳和固定的星球);一部关于行星及其运动;一部关于行星的物理属性与地理特征的形成(侧重于地球);一部是关于天空对地球的影响,涵盖大气光学、气象学和占星术。[20]
他还收集许多他曾经赠送《宇宙的神秘》的天文学家们的意见,其中包括瑞玛奴斯·乌尔苏斯(尼古拉斯·赖默斯·柏尔)[Reimarus Ursus(N. Reimers Bär)]——鲁道夫二世的皇家数学家,同时也是第谷·布拉赫的激烈对手。乌尔苏斯没有直接回复他,但是重新发表了开普勒的奉迎信,以寻求他与第谷关于第谷体系争论(现在的叫法)中的优势。尽管有这个污点,第谷还是开始与开普勒通信,一开始就对开普勒系统进行严厉但合理的批判;在许多反对的理由中,第谷对其使用哥白尼不准确的数据提出了异议。通过书信往来,第谷和开普勒就广大范围内的天文学问题进行了讨论,并重点讨论了月球现象与哥白尼学说(特别是其神学活力)。但是没有第谷天文台更精确的数据,开普勒无法涉及其中的许多议题。[21]
结果,开普勒将精力转向年代学与“和谐”,即音乐、数学及物质世界之间的命理关系,以及它们的占星结果。通过假设地球拥有精神(一种他后期用于解释太阳引起行星运动的属性),他建立了一个将占星内容和天文距离与天气与其它地球现象联系起来的推测系统。然而,到了1599年,他又发现他的工作受到数据不准确性的限制——正如不断增长的宗教紧张气氛正威胁他在格拉茨的工作一样。就在同年的12月份,第谷邀请开普勒在布拉格会面;1600年1月1日(甚至在他收到邀请函之前),开普勒就启程,希望第谷的资助能够帮解决他的哲学问题以及社会与经济问题。[22]
布拉格(1600-1612年)
[编辑]效力于第谷·布拉赫
[编辑]
1600年2月4日,开普勒在伊泽拉河畔贝纳特基(距离布拉格35km)见到了第谷·布拉赫及其助手弗朗茨·滕纳格尔(Franz Tengnagel)与朗高蒙田纳斯(Longomontanus)。伊泽拉河畔贝纳特基是第谷的新天文台所在地。开普勒以客人的身份在这里住了两个月,分析了第谷的一些火星发现;第谷严密地保护着他的数据,但是对开普勒的理论思想印象深刻,所以之后给了他更多接近的空间。开普勒计划借助火星数据测试他在《宇宙的神秘》中的理论[23],但是他预计这项工作将花费2年时间(因为第谷不允许他单纯的将资料拷贝作为己用)。在约翰内斯·杰森纽斯(Johannes Jessenius)的帮助下,开普勒尝试与第谷协商一个更为正式的雇佣安排,但是协商在激烈的争吵中破裂。于是开普勒在4月6日就前往布拉格。之后,开普勒和第谷很快就和解了,并最终就工资和生活安排达成了协议,6月,开普勒回到格拉茨去接他的家人。[24]
格拉茨政治上和宗教上的麻烦打碎了他立刻回到第谷天文台工作的想法;为了继续他的天文学研究,开普勒以数学家的身份向斐迪南大公寻求了一份工作。为此,开普勒专门写了一篇文章给斐迪南。他在文中提出了一个月球运动力学理论[25]:“地球上有一种力量,引起了月球的运动”。虽然这篇文章并未使他在费迪南宫廷获得职位,但是却详细介绍了一种测量月食的新方法,他将这种方法运用到了7月10日格拉茨的月食现象。这些观察成了他进行光学规律探索的基础,而《天文学的光学需知》则是他光学探索的顶峰。[26]
1600年8月2日,在拒绝皈依天主教之后,开普勒和他的家人被驱逐出格拉茨。几个月后,开普勒及他的家人来到了布拉格。差不多1601年一整年,他得到了第谷的直接资助,第谷安排他分析行星观测结果与编写反对第谷(此时第谷已过世)对手——乌尔苏斯的小册子。9月,第谷帮开普勒获得了作为他先前向皇帝提议的新项目的合作者的委任:将取代伊拉斯谟·赖因霍尔德所作的《普鲁士星表》的《鲁道夫星表》。1601年10月24日第谷出人意料的逝世了,两天之后,开普勒被委任成为他的继任者,作为皇家数学家负责完成第谷未完成的工作。接下去作为皇家数学家的11年是开普勒一生中最为多产的时间。[27]
皇帝鲁道夫二世的顾问
[编辑]作为皇家数学家,开普勒的主要职责是向皇帝提供占星术方面的建议。虽然开普勒对同时代占星家对未来或特定神学事件进行准确预言的努力采取怀疑态度,但是当他还是图宾根大学的一名学生时,他已经向他的朋友、家人和赞助人展示了极受欢迎的占星水平。除了给同盟国和外国领导人占星外,皇帝在遇到政治麻烦时,也向开普勒寻求建议。鲁道夫对许多其宫廷学者(包括炼金术士)的工作有着积极兴趣,并跟踪开普勒在物理天文学方面的工作。[28]
布拉格正式被认可的宗教教义是天主教和主稳健派,但是开普勒凭借他在宫廷的地位可以信仰他的路德教会而不受阻碍。皇帝名义上为其家庭提供了丰厚的收入,但是皇家国库开支过度,这意味着想要实际上获得足够的钱应对经济负担还是需要不断的争取。一部分源于经济困难的原因,他和芭芭拉的家庭生活并不如意,经常为争吵和疾病所扰。然而,宫廷生活为开普勒带来了与其他著名学者[其中包括约翰内斯·马修斯·瓦克·瓦克亨菲尔斯、约斯特·比尔吉、大卫·法布里奇乌斯、马丁·巴查杰克(M. Bachazek)以及约翰内斯·布伦格(Johannes Brengger)]接触的机会,因此他的天文学工作进展迅速。[29]
《天文学的光学需知》
[编辑]
在开普勒继续慢慢分析第谷的火星观测数据——现在他可以拥有整体的资料——并开始了鲁道夫星表的缓慢编制过程的同时,他还从其1600年关于月球的文章中拾起了对光学规律的研究。不论是月食或是日食现象都展现了无法解释的现象,例如不可预期的阴影大小、月全食的红色、以及传说中环绕日全食的罕见光线。大气折射的相关议题适用于所有天文学观测。1603年的大部分时间,开普勒暂停了他的其它工作,而专注于光学理论研究;并由此撰写的手稿在1604年1月1日呈给了皇帝,并以《天文学的光学需知》为题发表。文中,开普勒对控制光强的平方反比定律、平面镜与曲面镜的反射、针孔相机原理以及光学的天文学含义,如视差与天体的可见大小,进行了描述。他还将光学研究延伸到人的眼睛,并被神经学家广泛认为是意识到图像由眼睛晶状体翻转投射到视网膜上的第一人。这个困境的解决办法对于开普勒来说并不是特别重要,因为他并不将其视为属于光学的范畴,虽然他确实表明,影像由于“精神运动”在“脑穴”中得到修正[30]。今天,《天文学的光学需知》通常被认为是现代光学的基础(虽然它明显地没有包含折射定律)[31]。关于投影几何学的根源,开普勒在他作品中引入了数学实体连续变化的概念。他主张到,如果一个圆锥截面的焦点可以沿着连接焦点的线运动,那么这个几何形状会把一个焦点改变或退化成另外一个。因此,当一个焦点沿着无穷大运动时,椭圆形就变成了一条抛物线,当一个椭圆的两个焦点互相融合时,就形成了圆圈。
超新星1604
[编辑]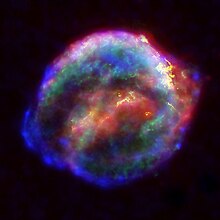
1604年10月,出现了一颗明亮的新晚星(超新星1604),但是开普勒不信谣言,直至他亲眼看到了这颗晚星。他开始系统的观察这颗新星。从星相学的角度看,1603年的结束标志着火象三星座的开始,亦即周期800年的大交汇期的开始;占星家们将之前两次这种时期与查理曼大帝的崛起(大约800年前)和耶稣的诞生(大约1600年前)联系起来,所以他们期待有重大预兆的事件出现,特别是关于皇帝。正是在这种情况下,开普勒作为皇家数学家与占星家在其两年后《关于新星》的文中描述了这颗新星。文中,开普勒在对其他许多占星方面的解释与流传持怀疑态度的同时,专注于描述这颗新星的天文学属性。他注意到了其逐渐减弱的亮度,推测它的起源,并根据视差的缺失论证它属于固定的星体,进一步削弱了天体永恒性的教义(自亚里斯多德以后人们一直认可这样的观念:天体是完美与永恒的)。一颗新星的诞生意味着天体的可变性。在附录中,开普勒还讨论了波兰历史学家劳伦休斯·苏斯莱格最近的年代学工作;他计算到,如果苏斯莱格是正确的,年表提前四年,那么伯利恒之星——类似于今日的新星——将已经正好碰到了周期800年的第一次大交汇。[32]
《新天文学》
[编辑]《新天文学》是根据第谷的方向进行的火星轨道研究(包括最初两个关于行星运动的定律)发展的顶峰。开普勒运用等分点(哥白尼把这种数学工具排除在他的学说之外)对各种安火星轨道近似值进行重复计算,并最终创造了一个在2弧分之内(平均测量误差)基本上与第谷的发现相一致的模型。但是他对这个复合体以及仍然有点不准确的结果感到不满意;在某些点,这个模型与数据的差异达到8弧分。一系列传统的数学天文学方法都使开普勒感到失望,他开始尝试为这些数据设置一个卵形轨道。[33]
根据开普勒对宇宙的宗教观点,太阳(父神的象征)是太阳系的动力来源。作为物理基础,开普勒通过类比汲取了威廉·吉尔伯特《论磁石》(1600年)中地球磁性灵魂的理论以及自己关于光学研究的工作。他假设太阳发射的动力(或动力个体)[34]随着距离减弱,当行星靠近或远离太阳,运动会加快或减慢[35][36]。可能这个设想的前提需要一种修复天文学秩序的数学关系。根据对地球和火星远日点和近日点的测量,他创立了一个公式。根据这个公式,行星的运动速度与它距太阳的距离成反比。然而,想要在整个轨道周期证实这种关系,需要进行非常广的计算;为简化计算任务,1602年底,开普勒运用几何学重新阐述了这个比例:行星在同样的时间内扫过同样的面积——开普勒关于行星运动的第二定律。[37]

之后,他运用几何速率法则,假定轨道是蛋形轨道,开始计算火星的整体轨道。在经历大约40次的尝试失败以后,1605年初,他最终偶然想到了椭圆形这个概念,他之前认为这个解决方法太简单,以至于早期的天文学家们都忽略了[來源請求]。在发现椭圆形轨道适用于火星的数据之后,他立即推断出所有行星都以太阳为中心按照椭圆形运动——开普勒关于行星运动的第一定律。然而,他没有聘用计算方面的助手,所以他未将该数学分析扩展到火星之外。当年年底,他完成了《新天文学》的手稿,但是由于第谷天文台使用(第谷后人的财产)的法律争议,直到1609年才发表。[38]
《折射光学》、《梦》及其它著作
[编辑]在《新天文学》完稿之后的几年,开普勒大部分的研究都集中在《鲁道夫星表》的编撰以及基于该星表的一整套星历(对行星和星位的具体预言,但是这两项工作在多年之后都没完成)。他还尝试(不成功)与意大利天文学家乔凡尼·安东尼奥·马吉尼(Giovanni Antonio Magini)的合作。他的其它作品涉及年代学(特别是耶稣一生中事件的日期记录)与占星学[特别是对轰动性的大灾难预言的批判,比如哈利萨耶斯·罗斯林(Helisaeus Roeslin)的预言]。[39]

正当开普勒和罗斯林忙于发表一系列攻击与回击时,菲利普·法赛里尔斯医生(P. Feselius)发表了一部作品,对占星学进行了全面地反驳(特别是罗斯林的作品)。一方面是出于对其所认为是占星学的多余的回应,另一方面是出于对过度的反对声音的回应,开普勒撰写了《第三方调解》。表面上,这篇文章——主要是给罗斯林和法赛里尔斯的普通赞助人看的——是对争论的学者之间的一次中立调解,但是文中体现了开普勒对占星学价值的基本观点,文章包含了行星与个体精神之间互动的一些假设机制。开普勒认为多数传统的占星学法则与方法是被“一只勤劳的母鸡”扒烂的“臭粪”,但是实际上认真的科学的占星家“偶尔会找到谷粒,甚至是珍珠或金块”。[40]

1610年的头几个月,伽利略用他强大的新望远镜,发现了四颗绕着木星运动的卫星。在发表他的报告——《星夜的差使》时,伽利略咨询了开普勒的意见,某种程度上是为了增加其观测发现的可信度。开普勒给予了积极的回应,撰写并发表了一篇简短的回复——《与星夜信使的对话》。他支持伽利略的观测,并对伽利略的发现以及望远镜观测方法对于天文学和光学以及宇宙学和占星学的含义进行了一系列的推断。同年年底,开普勒在《四颗卫星的观测报告》中发表了其利用望眼镜对月球的发现,进一步支持伽利略的发现。但是令开普勒失望的是,伽利略从未发表过其对《新天文学》的(任何)反应。[41]

在听说了伽利略用望远镜得到的发现之后,开普勒从科隆欧内斯特(Ernest)公爵那里借来了一个望远镜,开始对望远镜光学进行理论和实验研究[42]。1610年9月,作为研究成果的手稿完成,并在1611年以《折射光学》为题发表。文中,开普勒提出了双凸会聚透镜与双凹发散透镜的理论基础——以及它们如何组合制作出一个伽利略望远镜——以及真实与虚拟影像、直立与倒立影像的概念和焦距对放大与缩小的影响。他还介绍了一个改进型的望远镜——现在称为天文望远镜或开普勒望远镜——该望远镜有两个凸透镜,可以比伽利略的凸凹组合透镜产生更大的放大率。[43]
1611年左右,开普勒传阅了他的一份手稿,这份手稿最终以《梦》为题(在他过世之后)发表。这篇文章的部分目的是想描述从另外一个星球的视角来看,时下的天文学会是什么样子,以说明非地心学说的可行性。这份在转手几次后丢失了的手稿描述了一次神奇的月球之旅;它一部分是寓言,一部分是自传,一部分是星际之旅的专著(有时候也被称为第一部科幻作品)。多年之后,该故事的一份扭曲的版本引发了一场针对自己母亲的审巫案,起因是故事讲述者的母亲向一名恶魔学习太空旅行的方法。随着他母亲最终被判无罪,开普勒为该故事撰写了223个脚注——比实际的文本长7倍——对故事中隐藏的寓言性内容以及很多科学内容(尤其是关于月球地理)进行了解释。[44]
数学和物理学方面的工作
[编辑]作为那年新年的礼物,他为他的朋友也是多年的赞助人——瓦克·瓦克亨菲尔斯男爵,写了一本简短的小册子,题为《新年礼物——六角雪花》。文中,他发表了他首次对雪花六角对称性的描述,并将该问题扩展成为对称性的一个假设性原子论物理基础,并造就了后来人们所知道的开普勒猜想——最有效的球体填充方法说明[45][46]。开普勒是将无限小应用到数学的先驱,请参考连续性定律。
个人及政治麻烦
[编辑]1611年,布拉格政治与宗教之间日益紧张的关系达到了白热化的程度。鲁道夫皇帝的健康状况也在衰退,被他的弟弟马蒂亚斯(Matthias)逼迫退位作为波西米亚国王。双方都寻求开普勒占星术方面的建议,他刚好利用这个机会向他们提出和解的政治建议(跟星象无多少关系,除了劝阻激烈行动的一般陈述之外)。然而,很清楚的是开普勒在马蒂亚斯宫廷的前景已变暗淡。[47]
就在同一年,芭芭拉感染了匈牙利斑疹热,之后开始突然发作。当芭芭拉正在康复的时候,开普勒的三个孩子都患了天花;6岁的弗里德里希最终夭折了。之后,开普勒写信给纽伦堡和帕多瓦的潜在赞助人。位于纽伦堡的图宾根大学,担心开普勒已经接触了违反《奥格斯堡信纲》与《协同信条》的加尔文主义异端学说,因而阻止他回归。而帕多瓦大学,在将要离职的伽利略的推荐下,希望开普勒能够填补数学教授职位的空缺,但是开普勒不喜欢他的家庭离开德国的领土,因而他来到了奥地利的林茨,确定在这里当一名教师和教区数学家。然而,芭芭拉病情再次复发,在开普勒回去之后不久就去世了。[48]
开普勒推迟了搬到林茨的计划,继续留在布拉格直到鲁道夫于1612年初去世。同时遭遇了政治剧变、宗教紧张以及家庭悲剧(以及关于他妻子财产的法律纠纷),开普勒无法继续做研究。所以他将他的书信及早期的作品拼凑成了一份编年手稿——《编年纪选集》。在马蒂亚斯继任神圣的罗马皇帝之后,马蒂亚斯重新确认了开普勒皇家数学家的职位(及薪奉)并允许他搬到林茨。[49]
林茨和其它地方(1612年-1630年)
[编辑]
在林茨,开普勒的主要职责(不包括完成《鲁道夫星表》)是在教区学校任教并提供占星术和天文学服务。在那里的头些年,相比在布拉格的生活,他的经济条件更宽松,宗教更自由,虽然鉴于他神学上的顾虑,路德会教堂禁止他参加圣餐。他在林茨发表的第一部作品为《德维罗纪元》(1613),该作品对耶稣诞生的年份进行了进一步的阐释;他还参加审议,确定是否将教宗額我略十三世改革的历法引入新教徒的德国地区;同年,他还写了影响巨大的数学著作《求酒桶体积之新法》。该著作发表于1615年,介绍了测量容器容积的方法,如酒桶。[50]
第二段婚姻
[编辑]1613年10月30日,开普勒娶了24岁的苏珊娜·罗伊特林格(S. Reuttinger)。在其第一任妻子芭芭拉死后,开普勒在两年间已经考虑了11个不同的对象(做决定的过程后来成了婚姻问题)[51]。他最终回过头来选择了罗伊特林格(第五个对象)。对她,开普勒曾写道[52],“她用爱、谦逊的忠诚、节俭持家、勤劳及给继子们的爱俘获了我”。他这段婚姻的前三个孩子(格丽塔·里贾纳(Margareta Regina)、凯塔琳娜与西博尔德(Sebald))在童年时代就夭折了。另外三个孩子存活下来并长大成人:克尔杜拉(Cordula,生于1621年);弗里德曼(Fridmar,生于1623年);希尔伯特(Hildebert,生于1625年)。根据开普勒传记的作者,开普勒这段婚姻比第一段幸福。[53]
《哥白尼天文学概要》、历法以及其母亲审巫案
[编辑]
自从完成了《新天文学》之后,开普勒就开始计划编制天文学教科书[54]。1615年,他完成了《哥白尼天文学概要》三卷中的第一卷;第一卷(第1-3册)在1617年印刷,第二卷(第四册)1620年印刷,第三卷(第5-7册)在1621年印刷。尽管这个书名简单涉及了太阳中心说,开普勒的这套教科书成了他自己椭圆定律的巅峰之作,是其最富影响力的作品。它包含了全部三条行星运动定律,并尝试用物理因素解释天体运动[55]。虽然它明确的将行星运动的头两条定律(在《新天文学》中适用于火星)扩展到其它行星、月球及木星的美第奇卫星[56],但是它并没有解释椭圆轨道如何从观测资料中获取[57]。
作为《鲁道夫星表》与相关的星历的副产品,开普勒发表了天文历法,这套历法非常受欢迎,并抵消了他创作其它作品的费用,特别是当皇家国库的资助被中止后。根据他的历法,1617年-1624年间的6年中,开普勒预测了行星位置和天气以及政治事件;后者经常非常准确,得益于他敏锐的掌握了那个时期政治与神学的紧张关系。然而到1624年,紧张关系的升级以及预言的不准确意味着给开普勒自身带来的政治麻烦;他最后的历法在格拉茨被公开烧毁。[58]
1615年,一个与开普勒的弟弟克利斯朵夫(Christoph)产生经济纠纷、名叫厄休拉·莱因戈尔德(Ursula Reingold)的女子,声称开普勒的母亲卡塔琳娜用一种邪恶的饮料致使她生病。之后,争吵升级,1617年,卡塔琳娜被控施行巫术;审巫案在该时期的中欧非常普遍。从1620年8月开始,她被囚禁了14个月。1621年10月,她被释放,一部分原因是开普勒所进行的广泛的法律辩护。原告没有证据,只有谣言。卡塔琳娜遭受了言语恫吓(形象描述等待她的、施予女巫的折磨),以最终逼迫她认罪。在这次审判期间,开普勒推迟了他的其它工作,转而专注于他的“和谐理论”,并在1619年发表了他的成果——《世界的和谐》。[59]
《世界的和谐》
[编辑]开普勒深信“几何事物向造物主提供了装饰整个世界的模型”[60]。在《世界的和谐》中,他尝试用音乐解释自然世界的比例,特别是天文学与占星学方面[61]。“和谐”的中心是“天体音乐”,而毕达哥拉斯、托勒密以及开普勒之前的许多人都对“天体音乐”进行过研究;实际上,在《世界的和谐》刚发表之后,开普勒就卷入了与罗伯特·弗勒德(R. Fludd)的先后顺序纠纷,因为后者最近刚发表了他的和谐理论。[62]
开普勒从研究正多边形和多面体开始,包括后来被人们所熟知的开普勒多面体。从那里,他把他的和谐分析扩展到音乐、气象学和占星学;和谐产生于天体灵魂所作的音调,对于占星学来说,和谐源于这些音调与人类灵魂的互动。在这部作品的最后部分(第5册),开普勒介绍了行星运动,特别是轨道速度与距太阳的轨道距离之间的关系。其它天文学家也使用了类似的关系,但是开普勒利用第谷的资料和他自己的天文学理论,更加准确的处理这些关系,并赋予了他们新的物理学意义。[63]
在许多其它和谐中,开普勒清楚的说明了人们所知的行星运动第三定律。之后,他尝试了许多组合,直到发现(近似地)“周期的平方与平均距离的平方成正比”。虽然他给出了这次发现的日期(1618年3月8日),但是并未详细描述他是如何得出这个结论的[64]。然而,直到17世纪60年代,人们才意识到该纯力学定律对于行星动力学的更广泛的意义。当该法则与克里斯蒂安·惠更斯刚发现的离心力定律结合时,它就能使艾萨克·牛顿、爱德蒙·哈雷、甚至克里斯多佛·雷恩(C. Wren)和罗伯特·虎克独立的论证太阳与其行星之间假定的万有引力随着它们之间的距离的平方的减少而减少[65]。这就否定了学术物理学传统的假设——不论在什么时间,万有引力不随两个天体之间的距离改变而改变,正如开普勒所做的假设以及伽利略错误的普遍规律,即自由落体运动加速度是一样的,以及如伽利略的学生——波蕾莉(Borrelli)在其1666年的天体力学中所描述的一样[66]。威廉·吉尔伯特在用磁铁做实验之后,确定地球的中心是一块巨大的磁铁。他的理论引导开普勒认为太阳的磁力驱动行星在它们自己的轨道运动。这是对行星运动的一个有趣的解释,但是对开普勒来说,很不幸,这种解释是错的。在找到正确的答案之前,科学家们需要对运动有更多的了解。

《鲁道夫星表》及开普勒晚年
[编辑]1623年,开普勒最终完成了《鲁道夫星表》,这在当时被认为是他主要的工作。然而,由于皇帝的出版要求以及与第谷后人之间的协商,该星表直到1627年才开始印刷。同时,宗教紧张——正在发生的“三十年戰爭”的根源——再一次使开普勒及他的家人陷入危险的境地。1625年,天主教反改革派的代理人将开普勒大部分的藏书查封,1626年,林茨城被包围。开普勒搬到乌尔姆,在那里他自费印刷了该星表。[67]
1628年,随着皇帝费迪南德的军队在华伦斯坦将军的指挥下获得军事上的胜利,开普勒成为华伦斯坦的官方顾问。虽然本质上不是将军府的占星家,但是开普勒为华伦斯坦的占星家们提供天文学计算,并偶尔为华伦斯坦本人撰写天宫图。在他生命的最后几年,开普勒花了很多时间旅行,从布拉格皇宫到林茨,从乌尔姆到扎甘临时的家,以及最后到雷根斯堡。到雷根斯堡不久以后,开普勒就患病了。他于1630年11月15日去世,并安葬在那里;它安葬的地点在瑞典军队毁坏墓地之后不再存在[68]。只有开普勒自创的墓志铭还流传下来:
- Mensus eram coelos, nunc terrae metior umbras
- Mens coelestis erat, corporis umbra iacet.
- “我曾测天高,今欲量地深。”
- “我的灵魂来自上天,凡俗肉体归于此地。”[69]
对开普勒天文学的认可
[编辑]开普勒的定律并没有立即得到认可。几个重要人物如伽利略和勒内·笛卡尔完全忽视了开普勒的《新天文学》。许多天文学家,包括开普勒的老师——迈克尔·马斯特林,反对开普勒将物理学引入天文学。一些人采取了折中立场。关于椭圆的虚焦点,伊斯梅尔·布罗(Ismael Boulliau)认可椭圆轨道但是用均匀运动代替开普勒的面积定律,而塞斯·沃德(Seth W.)则使用等径运动的椭圆轨道。[70][71][72]
几位天文学者对开普勒的理论进行了试验,对其的各种修改违背了天文观测的结果。在这两颗行星没法正常观测到的情况下,金星与水星的两次凌日为开普勒的理论做了灵敏的试验。1631年的水星凌日,开普勒极其不确定水星的参数,建议观测者在预测日期的前一天与后一天寻找凌日现象。皮埃尔·伽桑狄在预测的日期观察到了凌日现象,证实了开普勒的预测[73]。这是首次观测到水星凌日。然而,他试图在一个月以后观测金星凌日,却因为《鲁道夫星表》的误差而失败。伽桑狄并未意识到那次的凌日现象并非在欧洲的大部分地方都可以观测得到,包括巴黎[74]。杰雷米亚·霍罗克斯在1639年观测到了金星凌日。在这之前,他用自己的观测结果修改了开普勒模型的参数,并预测了这次凌日现象,然后制作了观测工具。他一直是开普勒模型的坚定支持者[75][76][77]。
全欧洲的天文学者们都阅读了《哥白尼天文学概要》。开普勒死后,该书成为传播其思想的主要工具。1630-1650年间,该书成为使用最多的天文学教科书,使许多人改信椭圆为基础的天文学[55]。然而,很少人接受他建立于物理基础上的天体运动的观点。在17世纪后期,许多从开普勒的著作产生出来的物理天体学理论——尤其是乔瓦尼·阿方索·博雷利和罗伯特·虎克的理论——开始包含引力(虽然不是开普勒假定的准精神运动类)和笛卡尔惯性概念。而牛顿的《数学原理》则是这些理论的顶峰,在该著作中,牛顿从以力为基础的万有引力定律得出了开普勒行星运动定律[78]。
历史和文化遗产
[编辑]
开普勒在哲学和科学编史学方面的作用超出了其在天文学与自然哲学的历史发展中的作用。开普勒及其天体运动定律对早期的天文学史非常重要,比如孟都克拉(Jean-Étienne Montucla)1758年的《数学历史》以及德朗布爾(Jean-Baptiste Delambre)1821年的《现代天文学历史》。这些和其它从启蒙运动的视角编写的历史以怀疑和反对的态度看待开普勒的形而上学和宗教主张,但是到了后来的浪漫时期,自然哲学家们将这些元素视为他成功的关键。威廉姆·维赫维尔在他有着重要影响力的作品《归纳法科学的历史》(1837年)中,发现开普勒是归纳法科学天才的原型;在他的作品《哲学与归纳科学》(1840年)中,维赫维尔将开普勒称为科学方法最高级形式的体现。类似地,在凯瑟琳皇后购买了开普勒手稿之后第一个对其进行广泛研究的人——恩斯特·弗里德里希·阿贝尔特(Ernst F. Apelt)认定开普勒是“科学革命”的钥匙。阿贝尔特看过开普勒的关于数学、美感、物理学以及作为整个思想体系一部分的神学的观点,对开普勒的生活与工作首次进行了广泛的研究。[79]
19世纪末20世纪初,开普勒书籍出现了大量的现代翻译版本,而他的全集的系统出版则在1937年才开始(21世纪初才接近完成),麦克斯·凯斯帕(M. Caspar)撰写的开普勒自传于1948年出版[80]。然而,继阿贝尔特之后,亚历山大·柯瓦雷(A. Koyré)所写的关于开普勒的作品是对开普勒宇宙学及其影响进行历史解释的里程碑。20世纪30-40年代,科瓦雷以及第一代专业科学史学工作者中的其他许多人将“科学革命”描述为科学历史的核心事件,而开普勒是这场革命的核心人物(之一)。科瓦雷将开普勒的理论工作而不是实验工作置于从古代到现代世界观的知识转变过程的中心位置。自从20世纪60年代以后,对于开普勒的历史学术研究得到很大发展,涉及他的占星学与气象学、几何方法、他的宗教观在他工作中的作用、他的文学及修辞手法、他与同时期更广阔的文化与哲学思潮的互动,甚至是他作为一名科学历史学家的作用[81]。
对于开普勒在“科学革命”中的地位的争论也产生了一系列哲学和大众的作品。其中亚瑟·凯斯特勒所作的《梦游者》(1959)是最具影响力的作品之一。在该作品中,开普勒无疑是这场革命的英雄(不管是道德上、神学上或认知上)[82]。科学哲学家,如查尔斯·桑德斯·皮尔斯、诺伍德·拉塞尔·汉森(Norwood R. Hanson)、史蒂芬·图尔明(S. Toulmin)与卡尔·波珀都重复的求助于开普勒:不可比性实例、类比推理、证伪性与许多其它的哲学概念都在开普勒的作品中出现过。物理学家沃尔夫冈·泡利甚至使用开普勒与罗伯特·弗勒德的先后之争来探究分析心理学对科学研究的意义[83]。约翰·博纳维尔(J. Banville)所作的非常受欢迎的甚至是玄幻的历史小说《开普勒》(1981),对凯斯特勒(Koestler)的叙事性非小说与科学哲学中的许多主题进行了探究[84]。更为玄幻的是最近的一部非小说类作品——《天国的密谋》(2004),该书声称开普勒谋杀了第谷以获取他的数据[85]。开普勒获得了作为科学现代性的象征与超出时代的人物的大众形象;科普作家卡尔·萨根称他为“第一个天体物理学家与最后一个科学占星家”[86]。
德国作曲家保罗·欣德米特写了一部关于开普勒的歌剧——《世界的和谐》,以及一首源于该歌剧音乐的同名交响乐。
在奥地利,开普勒留下的历史遗产使他成为一枚银质收藏币的图案之一:2002年9月10日的10欧元约翰内斯·开普勒银质硬币。该硬币的反面是开普勒的画像,他曾经在格拉茨及附近地区教学。开普勒私下与汉斯·乌尔里奇·艾根伯格亲王(Hans Ulrich von Eggenberg)熟识,他很可能对艾根伯格城堡的建造产生了影响(这枚硬币正面的图案)。硬币上,在他的前面镶嵌了一个《宇宙的神秘》中的球体与多面体模型。[87]
2009年美国国家航空和宇宙航行局将开普勒对天文学领域的贡献命名为“开普勒使命”。[88]
在新西兰的峡湾国家森林公园,也有一座群山以开普勒命名,称为“开普勒山”,以及一条穿过该群山的被称为“开普勒小道”的“三日步行道”。
纪念活动
[编辑]圣公会(美国)礼仪历的5月23日是纪念开普勒与哥白尼的节日。[89]
天文學著作
[编辑]

- 《宇宙的奧秘》(Mysterium cosmographicum,1596)
- 《关于占星术更坚实的基础》(De Fundamentis Astrologiae Certioribus,On Firmer Fundaments of Astrology (页面存档备份,存于互联网档案馆); 1601年)
- 《天文學的光学部分》(Astronomiae Pars Optica,1604)
- 《蛇夫座腳部的新星》(De Stella Nova in Pede Serpentarii,1604)
- 《新天文学》(Astronomia nova,1609)
- 《第三方调解》(Tertius Interveniens,1610年)
- 《与星夜信使的对话》(Dissertatio cum Nuncio Sidereo,1610年)
- 《折射光学》(Dioptrice,1611)
- 《六角的雪花》(De nive sexangula,1611年)
- 《这些年里,圣母玛利亚与永恒的耶稣基督展现了人类出生前的本性》(De vero Anno, quo aeternus Dei Filius humanam naturam in Utero benedictae Virginis Mariae assumpsit,1614)[90]
- 《编年纪选集》(Eclogae Chronicae,1615年,和《与星夜信使的对话》一起发表)
- 《求酒桶体积之新法》(Nova stereometria doliorum vinariorum,1615年)
- 《哥白尼天文学概要》(Epitome astronomiae Copernicanae,从1618-1621年分三部分发表)
- 《世界的和諧》(Harmonices Mundi,1618)
- 《宇宙的神圣秘密》(第二版,Mysterium cosmographicum,1621年)
- 《鲁道夫星表》(Tabulae Rudolphinae,1627)
- 《月亮之夢》(Somnium,1634年)
參見
[编辑]引用和注释
[编辑]- ^ Barker and Goldstein. "Theological Foundations of Kepler's Astronomy", pp. 112–13.
- ^ Kepler. New Astronomy, title page, tr. Donohue, pp. 26–7
- ^ Kepler. New Astronomy, p. 48
- ^ Epitome of Copernican Astronomy in Great Books of the Western World, Vol 15, p. 845
- ^ Stephenson. Kepler's Physical Astronomy, pp. 1–2; Dear, Revolutionizing the Sciences, pp. 74–78
- ^ Caspar. Kepler, pp. 29–36; Connor. Kepler's Witch, pp. 23–46.
- ^ 7.0 7.1 Koestler. The Sleepwalkers, p. 234(translated from Kepler's family horoscope).
- ^ Caspar. Kepler, pp. 36–38; Connor. Kepler's Witch, pp. 25–27.
- ^ Connor, James A. Kepler's Witch(2004), p. 58.
- ^ Barker, Peter; Goldstein, Bernard R. "Theological Foundations of Kepler's Astronomy", Osiris, 2nd Series, Vol. 16, Science in Theistic Contexts: Cognitive Dimensions(2001), p. 96.
- ^ Westman, Robert S. "Kepler's Early Physico-Astrological Problematic," Journal for the History of Astronomy, 32(2001): 227–36.
- ^ Caspar. Kepler, pp. 38–52; Connor. Kepler's Witch, pp. 49–69.
- ^ Caspar. Kepler, pp. 60–65; see also: Barker and Goldstein, "Theological Foundations of Kepler's Astronomy."
- ^ Barker and Goldstein. "Theological Foundations of Kepler's Astronomy," pp. 99–103, 112–113.
- ^ Caspar. Kepler, pp. 65–71.
- ^ Field. Kepler's Geometrical Cosmology, Chapter IV, p 73ff.
- ^ Dreyer, J.L.E. A History of Astronomy from Thales to Kepler, Dover Publications, 1953, pp. 331, 377–379.
- ^ Caspar, Kepler. pp. 71–75.
- ^ Connor. Kepler's Witch, pp. 89–100, 114–116; Caspar. Kepler, pp. 75–77
- ^ Caspar. Kepler, pp. 85–86.
- ^ Caspar, Kepler, pp. 86–89
- ^ Caspar, Kepler, pp. 89–100
- ^ Using Tycho's data, see 'Two views of a system' 互联网档案馆的存檔,存档日期2011-07-21.
- ^ Caspar, Kepler, pp. 100–08.
- ^ Caspar, Kepler, p. 110.
- ^ Caspar, Kepler, pp. 108–11.
- ^ Caspar, Kepler, pp. 111–22.
- ^ Caspar, Kepler, pp. 149–53
- ^ Caspar, Kepler, pp. 146–148, 159–177
- ^ Finger, "Origins of Neuroscience," p 74. Oxford University Press, 2001.
- ^ Caspar, Kepler, pp. 142–146
- ^ Caspar, Kepler, pp. 153–157
- ^ Caspar, Kepler, pp. 123–128
- ^ On motive species, see: Lindberg, "The Genesis of Kepler's Theory of Light," pp. 38–40
- ^ "Kepler's decision to base his causal explanation of planetary motion on a distance-velocity law, rather than on uniform circular motions of compounded spheres, marks a major shift from ancient to modern conceptions of science.... [Kepler] had begun with physical principles and had then derived a trajectory from it, rather than simply constructing new models. In other words, even before discovering the area law, Kepler had abandoned uniform circular motion as a physical principle." Peter Barker and Bernard R. Goldstein, "Distance and Velocity in Kepler's Astronomy", Annals of Science, 51 (1994): 59–73, at p. 60.
- ^ Koyré, The Astronomical Revolution, pp. 199–202
- ^ Caspar, Kepler, pp. 129–132
- ^ Caspar, Kepler, pp. 131–140; Koyré, The Astronomical Revolution, pp. 277–279
- ^ Caspar, Kepler, pp. 178–81
- ^ Caspar, Kepler, pp. 181–85. The full title is Tertius Interveniens, das ist Warnung an etliche Theologos, Medicos vnd Philosophos, sonderlich D. Philippum Feselium, dass sie bey billicher Verwerffung der Sternguckerischen Aberglauben nict das Kindt mit dem Badt aussschütten vnd hiermit jhrer Profession vnwissendt zuwider handlen, translated by C. Doris Hellman as "Tertius Interveniens, that is warning to some theologians, medics and philosophers, especially D. Philip Feselius, that they in cheap condemnation of the star-gazer's superstition do not throw out the child with the bath and hereby unknowingly act contrary to their profession."
- ^ Caspar, Kepler, pp. 192–197
- ^ Koestler, The Sleepwalkers p. 384
- ^ Caspar, Kepler, pp. 198–202
- ^ Lear, Kepler's Dream, pp. 1–78
- ^ Schneer, "Kepler's New Year's Gift of a Snowflake," pp. 531–45
- ^ Kepler, Johannes. Hardie, Colin , 编. De nive sexangula [The Six-sided Snowflake]. Oxford: Clarendon Press. 1966 [1611]. OCLC 974730.
- ^ Caspar, Kepler, pp. 202–204
- ^ Connor, Kepler's Witch, pp. 222–226; Caspar, Kepler, pp. 204–07
- ^ Caspar, Kepler, pp. 208–11
- ^ Caspar, Kepler, pp. 209–20, 227–240
- ^ Ferguson, Thomas S., Who solved the secretary problem ?, Statistical Science, 1989, 4 (3): 282–289 [2014-10-30], doi:10.1214/ss/1177012493, (原始内容存档于2021-04-18),
When the celebrated German astronomer, Johannes Kepler (1571-1630), lost his first wife to cholera in 1611, he set about finding a new wife using the same methodical thoroughness and careful consideration of the data that he used in finding the orbit of Mars to be an ellipse... The process consumed much of his attention and energy for nearly 2 years...
- ^ Quotation from Connor, Kepler's Witch, p 252, translated from an October 23, 1613 letter from Kepler to an anonymous nobleman
- ^ Caspar, Kepler, pp. 220–223; Connor, Kepler's Witch, pp. 251–54.
- ^ Caspar, Kepler, pp. 239–240, 293–300
- ^ 55.0 55.1 Gingerich, "Kepler, Johannes" from Dictionary of Scientific Biography, pp. 302–04
- ^ By 1621 or earlier, Kepler recognized that Jupiter's moons obey his third law.
Kepler contended that rotating massive bodies communicate their rotation to their satellites, so that the satellites are swept around the central body; thus the rotation of the Sun drives the revolutions of the planets and the rotation of the Earth drives the revolution of the Moon. In Kepler's era, no one had any evidence of Jupiter's rotation. However, Kepler argued that the force by which a central body causes its satellites to revolve around it, weakens with distance; consequently, satellites that are farther from the central body revolve slower. Kepler noted that Jupiter's moons obeyed this pattern and he inferred that a similar force was responsible. He also noted that the orbital periods and semi-major axes of Jupiter's satellites were roughly related by a 3/2 power law, as are the orbits of the six (then known) planets. However, this relation was approximate: the periods of Jupiter's moons were known within a few percent of their modern values, but the moons’ semi-major axes were determined less accurately.
Kepler discussed Jupiter's moons in his Epitome Astronomiae Copernicanae [Summary of Copernican Astronomy](Linz ("Lentiis ad Danubium"),(Austria): Johann Planck, 1622), book 4, part 2, page 554 (页面存档备份,存于互联网档案馆).(For a more modern and legible edition, see: Christian Frisch, ed., Joannis Kepleri Astronomi Opera Omnia, vol. 6 (Frankfurt-am-Main, (Germany): Heyder & Zimmer, 1866), page 361 (页面存档备份,存于互联网档案馆).)Original : 4) Confirmatur vero fides hujus rei comparatione quatuor Jovialium et Jovis cum sex planetis et Sole. Etsi enim de corpore Jovis, an et ipsum circa suum axem convertatur, non ea documenta habemus, quae nobis suppetunt in corporibus Terrae et praecipue Solis, quippe a sensu ipso: at illud sensus testatur, plane ut est cum sex planetis circa Solem, sic etiam se rem habere cum quatuor Jovialibus, ut circa corpus Jovis quilibet, quo longius ab illo potest excurrere, hoc tardius redeat, et id quidem proportione non eadem, sed majore, hoc est sescupla proportionis intervallorum cujusque a Jove: quae plane ipsissima est, qua utebantur supra sex planetae. Intervalla enim quatuor Jovialium a Jove prodit Marius in suo Mundo Joviali ista: 3, 5, 8, 13 (vel 14 Galilaeo)…Periodica vero tempora prodit idem Marius ista: dies 1. h. 18 1/2, dies 3 h. 13 1/3, dies 7 h. 3, dies 16 h. 18: ubique proportio est major quam dupla, major igitur quam intervallorum 3, 5, 8, 13 vel 14, minor tamen quam quadratorum, qui duplicant proportiones intervallorum, sc. 9, 25, 64, 169 vel 196, sicut etiam sescupla sunt majora simplis, minora vero duplis.
Translation :(4)However, the credibility of this [argument] is proved by the comparison of the four [moons] of Jupiter and Jupiter with the six planets and the Sun. Because, regarding the body of Jupiter, whether it turns around its axis, we don't have proofs for what suffices for us [regarding the rotation of ] the body of the Earth and especially of the Sun, certainly [as reason proves to us]: but reason attests that, just as it is clearly [true] among the six planets around the Sun, so also it is among the four [moons] of Jupiter, because around the body of Jupiter any [satellite] that can go farther from it orbits slower, and even that [orbit's period] is not in the same proportion, but greater [than the distance from Jupiter]; that is, 3/2(sescupla)of the proportion of each of the distances from Jupiter, which is clearly the very [proportion] as [is used for] the six planets above. In his [book] The World of Jupiter [Mundus Jovialis, 1614], [Simon] Mayr [1573-1624] presents these distances, from Jupiter, of the four [moons] of Jupiter: 3, 5, 8, 13(or 14 [according to] Galileo)… Mayr presents their time periods: 1 day 18 1/2 hours, 3 days 13 1/3 hours, 7 days 3 hours, 16 days 18 hours: for all [of these data] the proportion is greater than double, thus greater than [the proportion] of the distances 3, 5, 8, 13 or 14, although less than [the proportion] of the squares, which double the proportions of the distances, namely 9, 25, 64, 169 or 196, just as [a power of] 3/2 is also greater than 1 but less than 2.
- ^ Wolf, A History of Science, Technology and Philosophy, pp. 140–41; Pannekoek, A History of Astronomy, p 252
- ^ Caspar, Kepler, pp. 239, 300–01, 307–08
- ^ Caspar, Kepler, pp. 240–264; Connor, Kepler's Witch, chapters I, XI-XIII; Lear, Kepler's Dream, pp. 21–39
- ^ Quotation from Caspar, Kepler, pp. 265–266, translated from Harmonices Mundi
- ^ The opening of the movie Mars et Avril by Martin Villeneuve is based on German astronomer Johannes Kepler’s cosmological model from the 17th century, Harmonices Mundi, in which the harmony of the universe is determined by the motion of celestial bodies. Benoît Charest also composed the score according to this theory.
- ^ Caspar, Kepler, pp. 264–66, 290–93
- ^ Caspar, Kepler, pp. 266–90
- ^ Arthur I. Miller. Deciphering the cosmic number: the strange friendship of Wolfgang Pauli and Carl Jung. W. W. Norton & Company. March 24, 2009: 80 [March 7, 2011]. ISBN 978-0-393-06532-9. (原始内容存档于2015-05-04).
- ^ Westfall, Never at Rest, pp. 143, 152, 402–03; Toulmin and Goodfield, The Fabric of the Heavens, p 248; De Gandt, 'Force and Geometry in Newton's Principia', chapter 2; Wolf, History of Science, Technology and Philosophy, p. 150; Westfall, The Construction of Modern Science, chapters 7 and 8
- ^ Koyré, The Astronomical Revolution, p. 502
- ^ Caspar, Kepler, pp. 308–328
- ^ Caspar, Kepler, pp. 332–351, 355–61
- ^ Koestler, The Sleepwalkers, p. 427.
- ^ Applebaum, Wilbur. Keplerian Astronomy after Kepler: Researches and Problems. History of Science. 1996-12-01, 34 [2022-10-05]. (原始内容存档于2022-10-05).
- ^ Koyré, The Astronomical Revolution, pp. 362–364
- ^ North, History of Astronomy and Cosmology, pp. 355–60
- ^ Albert van Helden, "The Importance of the Transit of Mercury of 1631," (页面存档备份,存于互联网档案馆) Journal for the History of Astronomy, 7 (1976): 1–10.
- ^ HM Nautical Almanac Office. 1631 Transit of Venus. June 10, 2004 [August 28, 2006]. (原始内容存档于2006年10月1日).
- ^ Chapman, A. Jeremiah Horrocks, The Transit of Venus, and the 'New Astronomy' in Early Seventeenth-Century England. Quarterly Journal of the Royal Astronomical Society. 1990-09-01, 31 [2022-10-05]. ISSN 0035-8738. (原始内容存档于2022-10-05).
- ^ North, History of Astronomy and Cosmology, pp. 348–349
- ^ Applebaum, W.; Hatch, R. A. Boulliau Mercator and Horrocks Venus in Sole Visa - Three Unpublished Letters. Journal for the History of Astronomy. 1983-01-01, 14 [2022-10-05]. ISSN 0021-8286. doi:10.1177/002182868301400302. (原始内容存档于2022-10-05).
- ^ Kuhn, The Copernican Revolution, pp. 238, 246–252
- ^ Jardine, "Koyré’s Kepler/Kepler's Koyré," pp. 363–367
- ^ Gingerich, introduction to Caspar's Kepler, pp. 3–4
- ^ Jardine, "Koyré’s Kepler/Kepler's Koyré," pp. 367–372; Shapin, The Scientific Revolution, pp. 1–2
- ^ Stephen Toulmin, Review of The Sleepwalkers in The Journal of Philosophy, Vol. 59, no. 18 (1962), pp. 500–503
- ^ Pauli, "The Influence of Archetypical Ideas"
- ^ William Donahue, "A Novelist's Kepler," Journal for the History of Astronomy, Vol. 13 (1982), pp. 135–136; "Dancing the grave dance: Science, art and religion in John Banville's Kepler," English Studies, Vol. 86, no. 5 (October 2005), pp. 424–438
- ^ Marcelo Gleiser, "Kepler in the Dock", review of Gilder and Gilder's Heavenly Intrigue, Journal for the History of Astronomy, Vol. 35, pt. 4 (2004), pp. 487–489
- ^ Quote from Carl Sagan, Cosmos: A Personal Voyage, episode III: "The Harmony of the Worlds". Kepler was hardly the first to combine physics and astronomy; however, according to the traditional (though disputed) interpretation of the Scientific Revolution, he would be the first astrophysicist in the era of modern science.
- ^ Eggenberg Palace coin. Austrian Mint. [September 9, 2009]. (原始内容存档于2011年5月31日).
- ^ Ng, Jansen. Kepler Mission Sets Out to Find Planets Using CCD Cameras. DailyTech. July 3, 2009 [July 3, 2009]. (原始内容存档于2009年3月10日).
- ^ Calendar of the Church Year according to the Episcopal Church. Charles Wohlers. [October 17, 2014]. (原始内容存档于2000-08-23).
- ^ "...in 1614, Johannes Kepler published his book "De vero anno quo aeternus dei filius humanum naturam in utero benedictae Virginis Mariae assumpsit", on the chronology related to the Star of Bethlehem.", The Star of Bethlehem, Kapteyn Astronomical Institute
- The most complete biography of Kepler is Max Caspar's Kepler. Though there are a number of more recent biographies, most are based on Caspar's work with minimal original research; much of the information cited from Caspar can also be found in the books by Arthur Koestler, Kitty Ferguson, and James A. Connor. Owen Gingerich's The Eye of Heaven builds on Caspar's work to place Kepler in the broader intellectual context of early-modern astronomy. Many later studies have focused on particular elements of his life and work. Kepler's mathematics, cosmological, philosophical and historical views have been extensively analyzed in books and journal articles, though his astrological work—and its relationship to his astronomy—remains understudied.
参考资料
[编辑]- Andersen, Hanne; Peter Barker; and Xiang Chen. The Cognitive Structure of Scientific Revolutions, chapter 6: "The Copernican Revolution." New York: Cambridge University Press, 2006. ISBN 978-0-521-85575-4
- Armitage, Angus. John Kepler, Faber, 1966.
- Banville, John. Kepler, Martin, Secker and Warburg, London, 1981 (fictionalised biography)
- Barker, Peter and Bernard R. Goldstein: "Theological Foundations of Kepler's Astronomy". Osiris, Volume 16. Science in Theistic Contexts. University of Chicago Press, 2001, pp. 88–113
- Caspar, Max. Kepler; transl. and ed. by C. Doris Hellman; with a new introduction and references by Owen Gingerich; bibliographic citations by Owen Gingerich and Alain Segonds. New York: Dover, 1993. ISBN 978-0-486-67605-0
- Connor, James A. Kepler's Witch: An Astronomer's Discovery of Cosmic Order Amid Religious War, Political Intrigue, and the Heresy Trial of His Mother. HarperSanFrancisco, 2004. ISBN 978-0-06-052255-1
- De Gandt, Francois. Force and Geometry in Newton's Principia, Translated by Curtis Wilson, Princeton University Press 1995. ISBN 978-0-691-03367-9
- Dreyer, J. L. E. A History of Astronomy from Thales to Kepler. Dover Publications Inc, 1967. ISBN 978-0-486-60079-6
- Ferguson, Kitty. The nobleman and his housedog: Tycho Brahe and Johannes Kepler: the strange partnership that revolutionized science. London: Review, 2002. ISBN 978-0-7472-7022-5 – published in the US as: Tycho & Kepler: the unlikely partnership that forever changed our understanding of the heavens. New York: Walker, 2002. ISBN 978-0-8027-1390-2
- Field, J. V.. Kepler's geometrical cosmology. Chicago University Press, 1988. ISBN 978-0-226-24823-3
- Gilder, Joshua and Anne-Lee Gilder: Heavenly Intrigue: Johannes Kepler, Tycho Brahe, and the Murder Behind One of History's Greatest Scientific Discoveries, Doubleday(May 18, 2004). ISBN 978-0-385-50844-5 Reviews bookpage.com, crisismagazine.com
- Gingerich, Owen. The Eye of Heaven: Ptolemy, Copernicus, Kepler. American Institute of Physics, 1993. ISBN 978-0-88318-863-7(Masters of modern physics; v. 7)
- Gingerich, Owen: "Kepler, Johannes" in Dictionary of Scientific Biography, Volume VII. Charles Coulston Gillispie, editor. New York: Charles Scribner's Sons, 1973
- Greenbaum and Boockmann: "Kepler's Astrology", Culture and Cosmos Vol. 14. Special Double Issue, 2012.
- Jardine, Nick: "Koyré’s Kepler/Kepler's Koyré," History of Science, Vol. 38 (2000), pp. 363–376
- Kepler, Johannes. Johannes Kepler New Astronomy trans. W. Donahue, forward by O. Gingerich, Cambridge University Press 1993. ISBN 978-0-521-30131-2
- Kepler, Johannes and Christian Frisch. Joannis Kepleri Astronomi Opera Omnia(John Kepler, Astronomer; Complete Works), 8 vols.(1858–1871). vol. 1, 1858 (页面存档备份,存于互联网档案馆), vol. 2, 1859 (页面存档备份,存于互联网档案馆), vol. 3, 1860 (页面存档备份,存于互联网档案馆), vol. 6, 1866 (页面存档备份,存于互联网档案馆), vol. 7, 1868 (页面存档备份,存于互联网档案馆), Frankfurt am Main and Erlangen, Heyder & Zimmer, – Google Books
- Kepler, Johannes, et al. Great Books of the Western World. Volume 16: Ptolemy, Copernicus, Kepler, Chicago: Encyclopædia Britannica, Inc., 1952.(contains English translations by of Kepler's Epitome, Books IV & V and Harmonices Book 5)
- Koestler, Arthur. The Sleepwalkers: A History of Man's Changing Vision of the Universe.(1959). ISBN 978-0-14-019246-9
- Koyré, Alexandre: Galilean Studies Harvester Press 1977. ISBN 978-0-85527-354-5
- Koyré, Alexandre: The Astronomical Revolution: Copernicus-Kepler-Borelli Ithaca, NY: Cornell University Press, 1973. ISBN 978-0-8014-0504-4; Methuen, 1973. ISBN 978-0-416-76980-7; Hermann, 1973. ISBN 978-2-7056-5648-5
- Kuhn, Thomas S. The Copernican Revolution: Planetary Astronomy in the Development of Western Thought. Cambridge, MA: Harvard University Press, 1957. ISBN 978-0-674-17103-9
- Lindberg, David C.: "The Genesis of Kepler's Theory of Light: Light Metaphysics from Plotinus to Kepler." Osiris, N.S. 2. University of Chicago Press, 1986, pp. 5–42.
- Lear, John. Kepler's Dream. Berkeley: University of California Press, 1965
- M.T.K Al-Tamimi: Great collapse Kepler's first law, Natural Science 2 (2010), ISBN 2150 – 4091
- North, John. The Fontana History of Astronomy and Cosmology, Fontana Press, 1994. ISBN 978-0-00-686177-5
- Pannekoek, Anton: A History of Astronomy, Dover Publications Inc 1989. ISBN 978-0-486-65994-7
- Pauli, Wolfgang. Wolfgang Pauli —Writings on physics and philosophy, translated by Robert Schlapp and edited by P. Enz and Karl von Meyenn(Springer Verlag, Berlin, 1994). See section 21, The influence of archetypical ideas on the scientific theories of Kepler, concerning Johannes Kepler and Robert Fludd(1574–1637). ISBN 978-3-540-56859-9
- Schneer, Cecil: "Kepler's New Year's Gift of a Snowflake." Isis, Volume 51, No. 4. University of Chicago Press, 1960, pp. 531–545.
- Shapin, Steven. The Scientific Revolution. Chicago: University of Chicago Press, 1996. ISBN 978-0-226-75020-0
- Stephenson, Bruce. Kepler's physical astronomy. New York: Springer, 1987. ISBN 978-0-387-96541-3(Studies in the history of mathematics and physical sciences; 13); reprinted Princeton:Princeton Univ. Pr., 1994. ISBN 978-0-691-03652-6
- Stephenson, Bruce. The Music of the Heavens: Kepler's Harmonic Astronomy, Princeton University Press, 1994. ISBN 978-0-691-03439-3
- Toulmin, Stephen and June Goodfield. The Fabric of the Heavens: The Development of Astronomy and Dynamics. Pelican, 1963.
- Voelkel, James R. The Composition of Kepler's Astronomia nova, Princeton University Press, 2001. ISBN 978-0-691-00738-0
- Westfall, Richard S.. The Construction of Modern Science: Mechanism and Mechanics. John Wiley and Sons, 1971. ISBN 978-0-471-93531-5; reprinted Cambridge University Press, 1978. ISBN 978-0-521-29295-5
- Westfall, Richard S. Never at Rest: A Biography of Isaac Newton. Cambridge University Press, 1981. ISBN 978-0-521-23143-5
- Wolf, A. A History of Science, Technology and Philosophy in the 16th and 17th centuries. George Allen & Unwin, 1950.
外部链接
[编辑]- Johannes Kepler的作品 - 古騰堡計劃
- 互联网档案馆中约翰内斯·开普勒的作品或与之相关的作品
- Kommission zur Herausgabe der Werke von Johannes Kepler (页面存档备份,存于互联网档案馆)
- JohannesKepler.Info (页面存档备份,存于互联网档案馆) Kepler information and community website, launched on December 27, 2009
- Harmonices mundi("The Harmony of the Worlds")in fulltext facsimile; Carnegie-Mellon University
- Daniel A. Di Liscia. Johannes Kepler. 扎尔塔, 爱德华·N (编). 《斯坦福哲学百科全书》.
- De Stella Nova in Pede Serpentarii("On the new star in Ophiuchus's foot")in full text facsimile at Linda Hall Library
- Walter W. Bryant. Kepler - 古腾堡计划(1920 book, part of Men of Science series)
- Electronic facsimile-editions of the rare book collection at the Vienna Institute of Astronomy
- 开放目录项目中的“约翰内斯·开普勒”
- Audio – Cain/Gay (2010) Astronomy Cast (页面存档备份,存于互联网档案馆) Johannes Kepler and His Laws of Planetary Motion
- Christianson, Gale E., Kepler's Somnium: Science Fiction and the Renaissance Scientist (页面存档备份,存于互联网档案馆)
- Kollerstrom, Nicholas, Kepler's Belief in Astrology (页面存档备份,存于互联网档案馆)
- References for Johannes Kepler (页面存档备份,存于互联网档案馆)
- Plant, David, Kepler and the "Music of the Spheres"
- Kepler, Napier, and the Third Law (页面存档备份,存于互联网档案馆) at MathPages
- Calderón Urreiztieta, Carlos. Harmonice Mundi · Animated and multimedia version of Book V (页面存档备份,存于互联网档案馆)
- Reading the mind of God 1997 drama based on his life by Patrick Gabridge
- Johannes Kepler 2010 drama based on his life by Robert Lalonde
- 約翰·J·奧康納; 埃德蒙·F·羅伯遜, Johannes Kepler, MacTutor数学史档案 (英语)
- Online Galleries, History of Science Collections, University of Oklahoma Libraries (页面存档备份,存于互联网档案馆) High resolution images of works by and/or portraits of Johannes Kepler in .jpg and .tiff format.
- TabvlæRudolphinæ qvibvs astronomicæ scientiæ (页面存档备份,存于互联网档案馆)... Typis J. Saurii, 1627. From the Rare Book and Special Collections Division (页面存档备份,存于互联网档案馆) at the Library of Congress

